题目内容
 如图,平面直角坐标系中,O为坐标原点,点A(8,0)点B(0,6)在y轴正半轴上,∠OBA的角平分线交OA于点C.求:直线BC的解析式.
如图,平面直角坐标系中,O为坐标原点,点A(8,0)点B(0,6)在y轴正半轴上,∠OBA的角平分线交OA于点C.求:直线BC的解析式.考点:待定系数法求一次函数解析式
专题:
分析:作CD⊥AB于点D,可得直角三角形CDA,利用勾股定理求得CD长即为OC长,也就求得了点C的坐标.再设直线BC的解析式为y=kx+b,将B、C两点的坐标代入,利用待定系数法即可求解.
解答: 解:如图,作CD⊥AB于点D.
解:如图,作CD⊥AB于点D.
在△BOC与△BDC中,
,
∴△BOC≌△BDC(AAS),
∴OC=DC,OB=DB,
∵OA=8,OB=6,
∴AB=10,
∴AD=10-BO=4,AC=8-CD,
∵CD2+AD2=AC2,
∴CD=3,
∴OC=3,
∴点C的坐标为(3,0).
设直线BC的解析式为y=kx+b,
∵B(0,6),C(3,0),
∴
,
解得
,
∴直线BC的解析式为y=-2x+6.
 解:如图,作CD⊥AB于点D.
解:如图,作CD⊥AB于点D.在△BOC与△BDC中,
|
∴△BOC≌△BDC(AAS),
∴OC=DC,OB=DB,
∵OA=8,OB=6,
∴AB=10,
∴AD=10-BO=4,AC=8-CD,
∵CD2+AD2=AC2,
∴CD=3,
∴OC=3,
∴点C的坐标为(3,0).
设直线BC的解析式为y=kx+b,
∵B(0,6),C(3,0),
∴
|
解得
|
∴直线BC的解析式为y=-2x+6.
点评:本题考查了待定系数法求一次函数解析式,全等三角形的判定与性质,勾股定理.准确作出辅助线构造直角三角形求出OC的长度是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
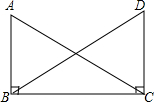 如图所示,已知AB=DC,∠ABC=∠DCB=90°,可以推得Rt△ABC≌Rt△DCB,所用的判断定理简称是( )
如图所示,已知AB=DC,∠ABC=∠DCB=90°,可以推得Rt△ABC≌Rt△DCB,所用的判断定理简称是( )| A、SAS | B、HL |
| C、ASA | D、AAS |
比较数的大小,下列结论错误的是( )
| A、-5<-3 | ||||||
B、-
| ||||||
| C、2>-3>0 | ||||||
D、-
|
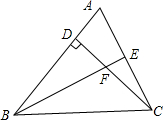 如图,△ABC中,∠ABC=45°,CD⊥AB于点D,E是AC的中点,连结BE交CD于F,且BF=AC.
如图,△ABC中,∠ABC=45°,CD⊥AB于点D,E是AC的中点,连结BE交CD于F,且BF=AC.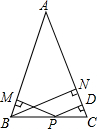 如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AC于点D,PM⊥AB于点M,BN为高,求证:PD+PM=BN.
如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AC于点D,PM⊥AB于点M,BN为高,求证:PD+PM=BN.