题目内容
 如图△ABC中,∠A=80°,∠B,∠C的角平分线交于点O,延长CO交AB于D,若∠ACD=30°,求∠DOB的度数.
如图△ABC中,∠A=80°,∠B,∠C的角平分线交于点O,延长CO交AB于D,若∠ACD=30°,求∠DOB的度数.考点:三角形内角和定理
专题:
分析:先根据角平分线的性质得出∠ACB的度数,再由三角形内角和定理求出∠ABC的度数,再由∠B,∠C的角平分线交于点O得出∠BCD及∠OBC的度数,由三角形外角的性质即可得出结论.
解答:解:∵CD是∠ACB的平分线,∠ACD=30°,∠A=80°,
∴∠ACB=2∠ACD=60°,
∴∠ABC=180°-80°-60°=40°.
∵∠B,∠C的角平分线交于点O,
∴∠OBC=
∠ABC=20°,∠OCB=∠ACD=30°.
∵∠DOB是△BOC的外角,
∴∠DOB=∠OBC+∠OCB=20°+30°=50°.
∴∠ACB=2∠ACD=60°,
∴∠ABC=180°-80°-60°=40°.
∵∠B,∠C的角平分线交于点O,
∴∠OBC=
| 1 |
| 2 |
∵∠DOB是△BOC的外角,
∴∠DOB=∠OBC+∠OCB=20°+30°=50°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
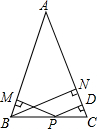 如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AC于点D,PM⊥AB于点M,BN为高,求证:PD+PM=BN.
如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AC于点D,PM⊥AB于点M,BN为高,求证:PD+PM=BN. 如图是某几何体的二视图,求它的表面积和体积.
如图是某几何体的二视图,求它的表面积和体积. 如图,在平面直角坐标系中,等边三角形ABC的边长为2.
如图,在平面直角坐标系中,等边三角形ABC的边长为2.