题目内容
 如图,⊙O是△ABC的外接圆,若AB=OA=OB,则∠C等于( )
如图,⊙O是△ABC的外接圆,若AB=OA=OB,则∠C等于( )| A、30° | B、40° |
| C、60° | D、80° |
考点:圆周角定理
专题:
分析:先根据AB=OA=OB得出△OAB是等边三角形,故∠AOB=60°,再由圆周角定理即可得出结论.
解答:解:∵AB=OA=OB,
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠C=
∠AOB=30°.
故选A.
∴△OAB是等边三角形,
∴∠AOB=60°,
∴∠C=
| 1 |
| 2 |
故选A.
点评:本题考查的是圆周角定理及垂径定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
两个相似三角形的相似比为4:5,较小的三角形有一边长为8厘米,则它所对应的较大三角形边长为( )
| A、5厘米 | B、10厘米 |
| C、15厘米 | D、20厘米 |
比较数的大小,下列结论错误的是( )
| A、-5<-3 | ||||||
B、-
| ||||||
| C、2>-3>0 | ||||||
D、-
|
在多边形一个外角等于60°,则这个多边形的边数为( )
| A、3 | B、4 | C、6 | D、8 |
下列整式中,( )是多项式.
| A、100t |
| B、v+2.5 |
| C、πr2 |
| D、0.1 |
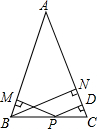 如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AC于点D,PM⊥AB于点M,BN为高,求证:PD+PM=BN.
如图,在△ABC中,AB=AC,P为BC上一点,PD⊥AC于点D,PM⊥AB于点M,BN为高,求证:PD+PM=BN. 如图,在平面直角坐标系中,等边三角形ABC的边长为2.
如图,在平面直角坐标系中,等边三角形ABC的边长为2.