题目内容
20. 如图所示,在△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,若AB=6cm,则△DEB的周长为( )
如图所示,在△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,若AB=6cm,则△DEB的周长为( )| A. | 12cm | B. | 8cm | C. | 6cm | D. | 4cm |
分析 先根据勾股定理求出BC的长,再由角平分线的性质得出DE=CD,进而可得出结论.
解答 解:∵在△ABC中,AC=BC,∠C=90°,AB=6cm,
∴BC2+AC2=AB2,即2BC2=36,解得BC=AC=3$\sqrt{2}$cm.
∵AD平分∠CAB交BC于点D,DE⊥AB于点E,
∴CD=DE.
在Rt△ACD与Rt△AED中,
∵$\left\{\begin{array}{l}CD=ED\\ AD=AD\end{array}\right.$,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=3$\sqrt{2}$cm,
∴BE=AB-AE=(6-3$\sqrt{3}$)cm,
∴△DEB的周长=(BD+DE)+BE=BC+BE=3$\sqrt{2}$+6-3$\sqrt{2}$=6cm.
故选C.
方法二:易知DE=DC,AC=AE=BC,
△BDE的周长=BD+DE+BE=(BD+DC)+BE=BC+BE=AE+BE=AB=6.
点评 本题考查的是等腰直角三角形,先根据题意得出BC的长是解答此题的关键.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
8.若kb<0,则直线y=kx+b一定通过( )
| A. | 第一、二象限 | B. | 第二、三象限 | C. | 第三、四象限 | D. | 第四、一象限 |
9.1的平方根是( )
| A. | 0 | B. | 1 | C. | ±1 | D. | -1 |
10.下列利用等式的性质,错误的是( )
| A. | 由a=b,得到5-2a=5-2b | B. | 由$\frac{a}{c}$=$\frac{b}{c}$,得到a=b | ||
| C. | 由a=b,得到ac=bc | D. | 由a=b,得到$\frac{a}{c}$=$\frac{b}{c}$ |
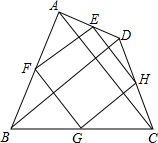 四边形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点
四边形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点
 如图的正方形地板,是由9块除颜色外完全相同的正方形地砖拼接而成的,其中黑色地砖5块,一个小球在这块地板上自由滚动,并随机地停在某块方砖上,它停留在黑色方砖上的概率为$\frac{5}{9}$.
如图的正方形地板,是由9块除颜色外完全相同的正方形地砖拼接而成的,其中黑色地砖5块,一个小球在这块地板上自由滚动,并随机地停在某块方砖上,它停留在黑色方砖上的概率为$\frac{5}{9}$. 如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,CD与BE交与点O、AD与BC交于点P、BE与CD交于点Q.
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,CD与BE交与点O、AD与BC交于点P、BE与CD交于点Q.