题目内容
8.先观察下列的计算,再完成习题:$\frac{1}{\sqrt{2}+1}$=$\frac{(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$$-\sqrt{2}$
$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\sqrt{4}$$-\sqrt{3}$
请你直接写出下面的结果:
(1)$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\sqrt{5}$-2;$\frac{1}{3+2\sqrt{2}}$=3-2$\sqrt{2}$;
(2)根据你的猜想、归纳,运用规律计算:
($\frac{1}{1+\sqrt{2}}$$+\frac{1}{\sqrt{2}+\sqrt{3}}$$+\frac{1}{\sqrt{3}+\sqrt{4}}$$+…+\frac{1}{\sqrt{2013}+\sqrt{2014}}$)×$(\sqrt{2014}+1$).
分析 (1)仿照已知等式将各式分母有理化即可;
(2)根据得出的规律将原式化简即可得到结果.
解答 解:(1)原式=$\frac{\sqrt{5}-\sqrt{4}}{(\sqrt{5}+\sqrt{4})(\sqrt{5}-\sqrt{4})}$=$\sqrt{5}$-2;
原式=$\frac{3-2\sqrt{2}}{(3+2\sqrt{2})(3-2\sqrt{2})}$=3-2$\sqrt{2}$;
故答案为:$\sqrt{5}$-2;3-2$\sqrt{2}$;
(2)原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2014}$-$\sqrt{2013}$)×($\sqrt{2014}$+1)
=($\sqrt{2014}$-1)×($\sqrt{2014}$+1)=2014-1=2013.
点评 此题考查了分母有理化,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
1.比$\frac{4}{7}$大且比$\frac{6}{7}$小的分数有( )
| A. | 一个 | B. | 两个 | C. | 无数个 | D. | 不存在 |
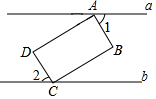 如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=66°,则∠2的度数为?
如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=66°,则∠2的度数为?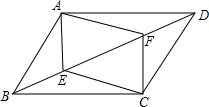 如图:在?ABCD中,E、F分别为对角线BD上的点,且BE=DF,判断四边形AECF的形状,并说明理由.
如图:在?ABCD中,E、F分别为对角线BD上的点,且BE=DF,判断四边形AECF的形状,并说明理由.