题目内容
2.已知关于x的方程$\frac{x-m}{2}$=x+$\frac{m}{3}$与$\frac{x+2}{3}$=3x-2的解互为倒数,求m的值.分析 求出第二个方程的解,利用倒数定义求出第一个方程的解,代入方程计算即可求出m的值.
解答 解:$\frac{x+2}{3}$=3x-2,
去分母得:x+2=9x-6,
移项合并得:8x=8,
解得:x=1,
把x=1代入方程$\frac{x-m}{2}$=x+$\frac{m}{3}$,得:$\frac{1-m}{2}$=1+$\frac{m}{3}$,
去分母得:3-3m=6+2m,
移项合并得:5m=-3,
解得:m=-0.6.
点评 此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
相关题目
13. 兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进20m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进20m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
 兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进20m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进20m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )| A. | (10$\sqrt{3}$+2)m | B. | (20$\sqrt{3}$+2)m | C. | (5$\sqrt{3}$+2)m | D. | (15$\sqrt{3}$+2)m |
7.已知a2-a=7,则代数式$\frac{a-1}{a+2}$•$\frac{{a}^{2}-4}{{a}^{2}-2a+1}$÷$\frac{1}{{a}^{2}-1}$的值是( )
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | 5 |
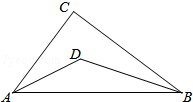 如图,在△ACB中,∠C=90°,∠CAB与∠CBA的角平分线交于点D,AC=3,BC=4,AB=5,则点D到AB的距离为1,则S△ABC=6.
如图,在△ACB中,∠C=90°,∠CAB与∠CBA的角平分线交于点D,AC=3,BC=4,AB=5,则点D到AB的距离为1,则S△ABC=6.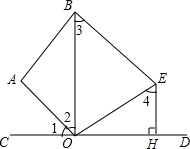 如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.
如图,已知∠1=∠2,OE⊥OA于点O,EH⊥CD于点H,∠3=∠4.求证:BE∥AO.