题目内容
12.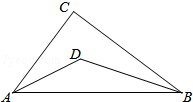 如图,在△ACB中,∠C=90°,∠CAB与∠CBA的角平分线交于点D,AC=3,BC=4,AB=5,则点D到AB的距离为1,则S△ABC=6.
如图,在△ACB中,∠C=90°,∠CAB与∠CBA的角平分线交于点D,AC=3,BC=4,AB=5,则点D到AB的距离为1,则S△ABC=6.
分析 作DE⊥AB于E,DF⊥BC于F,DG⊥AC于G,根据角平分线的性质得到DF=DG=DE=1,根据三角形面积公式计算即可.
解答 解: 作DE⊥AB于E,DF⊥BC于F,DG⊥AC于G,
作DE⊥AB于E,DF⊥BC于F,DG⊥AC于G,
∵∠CAB与∠CBA的角平分线交于点D,点D到AB的距离为1,
∴DF=DG=DE=1,
∴S△ABC=$\frac{1}{2}$×AB×1$+\frac{1}{2}×$BC×1$+\frac{1}{2}×$AC×1=6,
故答案为:6.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知⊙O的直径为8cm,圆心O到直线l的距离为4cm,则直线l和⊙O的位置关系是( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不能确定 |
20.如果一个一元二次方程的根是x1=x2=3,那么这个方程是( )
| A. | x2=3 | B. | x2-9=0 | C. | (x-3)2=0 | D. | (x+3)2=0 |
7. 如图,AB∥CD,AD∥BC,AC与BD相交于点O,则图中全等三角形共有( )
如图,AB∥CD,AD∥BC,AC与BD相交于点O,则图中全等三角形共有( )
 如图,AB∥CD,AD∥BC,AC与BD相交于点O,则图中全等三角形共有( )
如图,AB∥CD,AD∥BC,AC与BD相交于点O,则图中全等三角形共有( )| A. | 2对 | B. | 4对 | C. | 6对 | D. | 8对 |
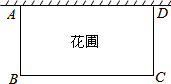 如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10 米),围成一个长方形的花圃.设花圃的宽AB为x米,面积为S平方米.
如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10 米),围成一个长方形的花圃.设花圃的宽AB为x米,面积为S平方米. 如图所示的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线.以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点,则抛物线的解析式是y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.
如图所示的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线.以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点,则抛物线的解析式是y=-$\frac{1}{9}$x2+$\frac{4}{3}$x.