题目内容
18.(1)$\frac{3x-5}{x-2}$=2-$\frac{x+1}{x-2}$(2)$\frac{x-2}{x+2}$-$\frac{12}{{x}^{2}-4}$=1
(3)$\frac{2}{x-1}$-$\frac{3}{x+1}$=$\frac{x+3}{{x}^{2}-1}$.
分析 各分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:3x-5=2x-4-x-1,
移项合并得:2x=0,
解得:x=0,
经检验x=0是分式方程的解;
(2)去分母得:(x-2)2-12=x2-4,
整理得:-4x=4,
解得:x=-1,
经检验x=-1是分式方程的解;
(3)去分母得:2x+2-3x+3=x+3,
解得:x=1,
经检验x=1是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
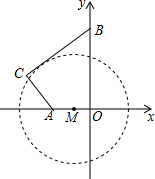 某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.
某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.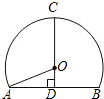 如图,若它的形状是以O为圆心的圆的一部分,AB=8,高CD=8,则半径OA等于5.
如图,若它的形状是以O为圆心的圆的一部分,AB=8,高CD=8,则半径OA等于5.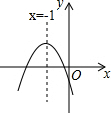 y=ax2+bx+c(a≠0)的图象如图所示,那么下面六个代数式:abc,b2-4ac,a-b+c,a+b+c,2a-b,9a-4b中,值大于0的有( )
y=ax2+bx+c(a≠0)的图象如图所示,那么下面六个代数式:abc,b2-4ac,a-b+c,a+b+c,2a-b,9a-4b中,值大于0的有( )