题目内容
9. 如图,在△ABC中,∠BAC=65°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=50°.
如图,在△ABC中,∠BAC=65°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=50°.
分析 根据旋转的性质得AC′=AC,∠B′AB=∠C′AC,再根据等腰三角形的性质得∠AC′C=∠ACC′,然后根据平行线的性质由CC′∥AB得∠ACC′=∠CAB=65°,则∠AC′C=∠ACC′=65°,再根据三角形内角和计算出∠CAC′=50°,所以∠B′AB=50°.
解答 解:解:∵△ABC绕点A逆时针旋转到△AB′C′的位置,
∴AC′=AC,∠B′AB=∠C′AC,
∴∠AC′C=∠ACC′,
∵CC′∥AB,
∴∠ACC′=∠CAB=65°,
∴∠AC′C=∠ACC′=65°,
∴∠CAC′=180°-2×65°=50°,
∴∠B′AB=50°,
故答案为50.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了平行线的性质.

练习册系列答案
相关题目
20.已知一个多项式与3x2+8x的和等于3x2+2x+4,则这个多项式是( )
| A. | 6x+4 | B. | -6x+4 | C. | 6x-4 | D. | -6x-4 |
4.关于一次函数y=-2x+b(b为常数),下列说法正确的是( )
| A. | y随x的增大而增大 | |
| B. | 当b=4时,直线与坐标轴围成的面积是4 | |
| C. | 图象一定过第一、三象限 | |
| D. | 与直线y=3-2x相交于第四象限内一点 |
14.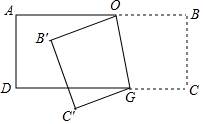 如图,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为( )
如图,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为( )
 如图,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为( )
如图,将长方形ABCD沿线段OG折叠到OB'C'G的位置,∠OGC'等于100°,则∠DGC'的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
1.一个事件的概率不可能是( )
| A. | $\frac{3}{2}$ | B. | 0 | C. | 1 | D. | $\frac{1}{3}$ |
18.已知函数y=(m+1)x${\;}^{{m}^{2}-3}$是正比例函数,且图象在第二、四象限内,则m的值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | -$\frac{1}{2}$ |
