题目内容
8．
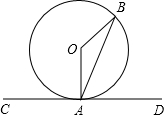如图，AB是⊙O的弦，CD与⊙O相切于点A，若∠BAD=66°，则∠B等于（ ）| A． | 24° | B． | 33° | C． | 48° | D． | 66° |
分析 因为OA=0B，所以∠B=∠AOB，欲求∠B，只要求出∠OAB的大小即可．
解答 解：∵CD与⊙O相切于点A，
∴OA⊥CD，
∴∠OAD=90°，
∵∠BAD=66°，
∴∠OAB=90°-∠BAD=24°，
∵OA=OB，
∴∠B=∠OAB=24°．
故选A．
点评 本题考查切线的性质、圆的性质，利用切线的性质以及半径相等是解题的关键，属于基础题中考常考题型．
练习册系列答案
相关题目
如图，菱形ABCD的对角线交于点O，AC=16cm，BD=12cm．
19．
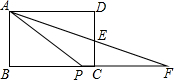在矩形ABCD中，AB=2，AD=4，E为CD的中点，连接AE交BC的延长线于F点，P为BC上一点，当∠PAE=∠DAE时，AP的长为（ ）
在矩形ABCD中，AB=2，AD=4，E为CD的中点，连接AE交BC的延长线于F点，P为BC上一点，当∠PAE=∠DAE时，AP的长为（ ）| A． | 4 | B． | $\frac{17}{4}$ | C． | $\frac{9}{2}$ | D． | 5 |
3．如果（an•bmb）3=a9b15，那么（ ）
| A． | m=4，n=3 | B． | m=4，n=4 | C． | m=3，n=4 | D． | m=3，n=3 |
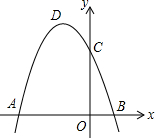如图，抛物线y=ax2+bx+c（a≠0）经过点A（-3，0），B（1，0），C（0，3）．
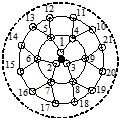课题研究小组对附着在物体表面的三个微生物（课题小组成员把他们分别标号为1，2，3）的生长情况进行观察记录．这三个微生物第一天各自一分为二，产生新的微生物（分别被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录）．那么标号为150的微生物会出现在（ ）