题目内容
19.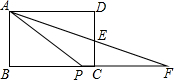 在矩形ABCD中,AB=2,AD=4,E为CD的中点,连接AE交BC的延长线于F点,P为BC上一点,当∠PAE=∠DAE时,AP的长为( )
在矩形ABCD中,AB=2,AD=4,E为CD的中点,连接AE交BC的延长线于F点,P为BC上一点,当∠PAE=∠DAE时,AP的长为( )| A. | 4 | B. | $\frac{17}{4}$ | C. | $\frac{9}{2}$ | D. | 5 |
分析 根据矩形的性质结合等角对等边,进而得出CF的长,再利用勾股定理得出AP的长.
解答 解:∵AD∥BC,
∴∠DAE=∠F,
又∵∠PAE=∠DAE,
∴∠PAE=∠F,
∴PA=PF,
∴CF=AD=4,
设CP=x,PA=PF=x+4,BP=4-x,
在直角△ABP中,
22+(4-x)2=(x+4)2,
解得:x=$\frac{1}{4}$,
∴AP的长为:$\frac{17}{4}$.
故选:B.
点评 此题主要考查了矩形的性质以及勾股定理等知识,正确得出FC的长是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
4. 寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:
寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:
根据统计图表信息解答下列问题:
(1)将条形统计图补充完整;
(2)若用扇形统计图来描述10名学生寒假体育锻炼情况,分别求A,B,C三个等级对应的扇形圆心角的度数;
(3)已知这次统计中共有60名学生寒假体育锻炼时间是A等,请你估计这次统计中B等,C等的学生各有多少名?
 寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:
寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:| 编号 | 成绩 | 编号 | 成绩 |
| ① | B | ⑥ | A |
| ② | A | ⑦ | B |
| ③ | B | ⑧ | C |
| ④ | B | ⑨ | B |
| ⑤ | C | ⑩ | A |
(1)将条形统计图补充完整;
(2)若用扇形统计图来描述10名学生寒假体育锻炼情况,分别求A,B,C三个等级对应的扇形圆心角的度数;
(3)已知这次统计中共有60名学生寒假体育锻炼时间是A等,请你估计这次统计中B等,C等的学生各有多少名?
8.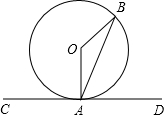 如图,AB是⊙O的弦,CD与⊙O相切于点A,若∠BAD=66°,则∠B等于( )
如图,AB是⊙O的弦,CD与⊙O相切于点A,若∠BAD=66°,则∠B等于( )
 如图,AB是⊙O的弦,CD与⊙O相切于点A,若∠BAD=66°,则∠B等于( )
如图,AB是⊙O的弦,CD与⊙O相切于点A,若∠BAD=66°,则∠B等于( )| A. | 24° | B. | 33° | C. | 48° | D. | 66° |
9.已知∠α=30°,那么∠α的余角等于( )
| A. | 30° | B. | 60° | C. | 70° | D. | 150° |
 “斗地主”是常见的一种游戏,一副扑克牌除大、小王外共有四种花色,每种花色从小到大共有牌面为3、4、5、6、7、8、9、10、J、Q、K、A、2的牌各一张(如图),现甲、乙、丙玩“斗地主”游戏,
“斗地主”是常见的一种游戏,一副扑克牌除大、小王外共有四种花色,每种花色从小到大共有牌面为3、4、5、6、7、8、9、10、J、Q、K、A、2的牌各一张(如图),现甲、乙、丙玩“斗地主”游戏,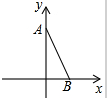 如图,在平面直角坐标系中,点A,B的坐标分别为(0,1)和$(\sqrt{3},0)$,若在第四象限存在点C,使△OBC和△OAB相似,则点C的坐标是($\sqrt{3}$,-1),或($\sqrt{3}$,3)或($\frac{\sqrt{3}}{4}$,-$\frac{3}{4}$)或($\frac{3\sqrt{3}}{4}$,-$\frac{3}{4}$).
如图,在平面直角坐标系中,点A,B的坐标分别为(0,1)和$(\sqrt{3},0)$,若在第四象限存在点C,使△OBC和△OAB相似,则点C的坐标是($\sqrt{3}$,-1),或($\sqrt{3}$,3)或($\frac{\sqrt{3}}{4}$,-$\frac{3}{4}$)或($\frac{3\sqrt{3}}{4}$,-$\frac{3}{4}$).


