题目内容
5．圆内接正六边形的边心距与半径之比是$\sqrt{3}$：2．分析 设正六边形的边长为2，欲求半径、边心距之比，我们画出图形，通过构造直角三角形，解直角三角形即可得出．
解答 解：如右图所示，
设边长AB=2；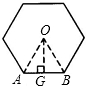
连接OA、OB，作OG⊥AB于G，
∵多边形为正六边形，
∴∠AOB=$\frac{360°}{6}$=60°，
∵OA=OB，
∴△AOB是等边三角形，
∴OA=AB=2，
在Rt△BOG中，BG=$\frac{1}{2}$AB=1，
∴OG=$\sqrt{3}$，
∴边心距与半径之比为$\sqrt{3}$：2．
故答案为：$\sqrt{3}$：2．
点评 本题考查了正多边形和圆；正多边形的计算一般是通过中心作边的垂线，连接半径，把正多边形中的半径，边长，边心距，中心角之间的计算转化为解直角三角形．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
如图，P是抛物线y=-x2+x+2在第一象限上的点，过点P分别向x轴和y轴引垂线，垂足分别为A，B，则四边形OAPB周长的最大值为6．
二次函数y=ax2+bx+c（a≠0，a、b、c为常数）的图象如图，则方程ax2+bx+c=m有实数根的条件是m≥-2．
13．
如图，在矩形ABCD中，AB=3，BC=4，对角线AC、BD相交于点O，过A作AE⊥BD交BD于点E，将△ABE沿AE折叠，点B恰好落在线段OD的F点处，则DF的长为（ ）
如图，在矩形ABCD中，AB=3，BC=4，对角线AC、BD相交于点O，过A作AE⊥BD交BD于点E，将△ABE沿AE折叠，点B恰好落在线段OD的F点处，则DF的长为（ ）| A． | $\frac{9}{5}$ | B． | $\frac{18}{5}$ | C． | $\frac{7}{5}$ | D． | $\frac{16}{5}$ |
