题目内容
15. 如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为6.
如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为6.
分析 设P(x,y)(2>x>0,y>0),根据矩形的周长公式得到C=-2(x-1)2+6.根据二次函数的性质来求最值即可.
解答 解:∵y=-x2+x+2,
∴当y=0时,-x2+x+2=0即-(x-2)(x+1)=0,
解得 x=2或x=-1
故设P(x,y)(2>x>0,y>0),
∴C=2(x+y)=2(x-x2+x+2)=-2(x-1)2+6.
∴当x=1时,C最大值=6,.
即四边形OAPB周长的最大值为6.
故答案是:6.
点评 本题考查了二次函数的最值,二次函数图象上点的坐标特征.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.本题采用了配方法.

练习册系列答案
相关题目
9. 体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:
体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:
(1)a=125,b=250;
(2)补全条形统计图;
(3)试估计这6000名九年级男生中50米跑到良好和优秀等级的总人数.
 体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:
体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:| 等级 | 人数/名 |
| 优秀 | a |
| 良好 | b |
| 及格 | 100 |
| 不及格 | 25 |
(2)补全条形统计图;
(3)试估计这6000名九年级男生中50米跑到良好和优秀等级的总人数.
7. 如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=6cm,DE=2cm,则BC的长为( )
如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=6cm,DE=2cm,则BC的长为( )
 如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=6cm,DE=2cm,则BC的长为( )
如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=6cm,DE=2cm,则BC的长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 12cm |


 在△ABC中,AB=6,BC=8,CA=7,延长CA至点P,使∠PBA=∠C,求AP的长.
在△ABC中,AB=6,BC=8,CA=7,延长CA至点P,使∠PBA=∠C,求AP的长. 如图,在平面直角坐标系中,以(6,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B和C,解答下列问题:
如图,在平面直角坐标系中,以(6,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B和C,解答下列问题: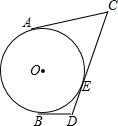 如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B.如果CD=7,AC=4,那么DB等于3.
如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B.如果CD=7,AC=4,那么DB等于3.