题目内容
13. 如图,在矩形ABCD中,AB=3,BC=4,对角线AC、BD相交于点O,过A作AE⊥BD交BD于点E,将△ABE沿AE折叠,点B恰好落在线段OD的F点处,则DF的长为( )
如图,在矩形ABCD中,AB=3,BC=4,对角线AC、BD相交于点O,过A作AE⊥BD交BD于点E,将△ABE沿AE折叠,点B恰好落在线段OD的F点处,则DF的长为( )| A. | $\frac{9}{5}$ | B. | $\frac{18}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{16}{5}$ |
分析 由矩形的性质得出∠BAD=90°,AD=BC=4,由勾股定理求出BD,由三角形的面积求出AE,由勾股定理得出BE,由翻折变换的性质得出EF=BE=$\frac{9}{5}$,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC=4,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=5,
∵AE⊥BD,
∴△ABD的面积=$\frac{1}{2}$AB•AD=$\frac{1}{2}$BD•AE,
∴AE=$\frac{AB×AD}{BD}$=$\frac{12}{5}$,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\frac{9}{5}$,
由翻折变换的性质得:EF=BE=$\frac{9}{5}$,
∴DF=BD-BE-EF=5-$\frac{9}{5}$-$\frac{9}{5}$=$\frac{7}{5}$.
故选:C.
点评 本题考查了矩形的性质、勾股定理、翻折变换的性质、三角形面积的计算;熟练掌握矩形和翻折变换的性质,由勾股定理求出BE是解决问题的关键.

练习册系列答案
相关题目
2.我们经常看到不文明踩踏草坪的现象,更令人痛心的是草坪是被踩出一条条直线的小路,用几何知识解释其道理正确的是( )
| A. | 两点确定一条直线 | B. | 两点之间线段最短 | ||
| C. | 垂线段最短 | D. | 三角形两边之和大于第三边 |

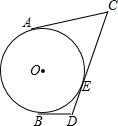 如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B.如果CD=7,AC=4,那么DB等于3.
如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B.如果CD=7,AC=4,那么DB等于3. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,有下列结论:
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,有下列结论: 每个小方格都是边长为1个单位长度,正方形ABCD在坐标系中的位置如图所示.
每个小方格都是边长为1个单位长度,正方形ABCD在坐标系中的位置如图所示.