题目内容
16．
二次函数y=ax2+bx+c（a≠0，a、b、c为常数）的图象如图，则方程ax2+bx+c=m有实数根的条件是m≥-2．
分析 由于抛物线y=ax2+bx+c与直线y=m有交点时，方程ax2+bx+c=m有实数根，观察函数图象得到当m≥-2时，抛物线y=ax2+bx+c与直线y=m有交点，从而得到方程ax2+bx+c=m有实数根的条件．
解答 解：当抛物线y=ax2+bx+c与直线y=m有交点时，方程ax2+bx+c=m有实数根，
因为直线y=-2与抛物线y=ax2+bx+c只有一个公共点，
所以当m≥-2时，抛物线y=ax2+bx+c与直线y=m有交点，
即方程ax2+bx+c=m有实数根的条件是m≥-2．
故答案为m≥-2．
点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．解决本题的关键是把方程ax2+bx+c=m有实数根问题转化为抛物线y=ax2+bx+c与直线y=m有交点的问题．
练习册系列答案
相关题目
9．
体能抽测小组从某市6000名九年级男生中，随机抽取了500名进行50米跑测试，并根据测试结果绘制了如下尚不完整的统计图表．解答下列问题：
（1）a=125，b=250；
（2）补全条形统计图；
（3）试估计这6000名九年级男生中50米跑到良好和优秀等级的总人数．
体能抽测小组从某市6000名九年级男生中，随机抽取了500名进行50米跑测试，并根据测试结果绘制了如下尚不完整的统计图表．解答下列问题：| 等级 | 人数/名 |
| 优秀 | a |
| 良好 | b |
| 及格 | 100 |
| 不及格 | 25 |
（2）补全条形统计图；
（3）试估计这6000名九年级男生中50米跑到良好和优秀等级的总人数．
7．
如图，在△ABC中，AB=AC，D、E是△ABC内的两点，AD平分∠BAC，∠EBC=∠E=60°．若BE=6cm，DE=2cm，则BC的长为（ ）
如图，在△ABC中，AB=AC，D、E是△ABC内的两点，AD平分∠BAC，∠EBC=∠E=60°．若BE=6cm，DE=2cm，则BC的长为（ ）| A． | 4cm | B． | 6cm | C． | 8cm | D． | 12cm |
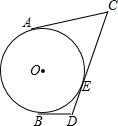如图，CD是⊙O的切线，切点为E，AC、BD分别与⊙O相切于点A、B．如果CD=7，AC=4，那么DB等于3．
11．
已知，如图，C、D是OA上两点，E、F是OB上两点，下列各式中，表示∠AOB错误的是（ ）
已知，如图，C、D是OA上两点，E、F是OB上两点，下列各式中，表示∠AOB错误的是（ ）| A． | ∠COE | B． | ∠AOF | C． | ∠DOB | D． | ∠EOF |
如图是二次函数y=ax2+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是x=1，有下列结论：
每个小方格都是边长为1个单位长度，正方形ABCD在坐标系中的位置如图所示．