题目内容
16. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=1.小夏同学给出了如下四个结论:①abc>0;②2a+b=0;③9a+3b+c<0;④(a+c)2>b2,并把它们分别写在四张相同卡片上,将卡洗匀后背面朝上,小东同学从中随机抽取一张,所抽卡片上的结论正确的概率为$\frac{1}{2}$.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=1.小夏同学给出了如下四个结论:①abc>0;②2a+b=0;③9a+3b+c<0;④(a+c)2>b2,并把它们分别写在四张相同卡片上,将卡洗匀后背面朝上,小东同学从中随机抽取一张,所抽卡片上的结论正确的概率为$\frac{1}{2}$.
分析 由抛物线开口方向得a<0,由抛物线的对称轴位置得b>0,由抛物线与y轴的交点位置得c>0,于是可对①进行判断;根据抛物线的对称轴为直线x=-$\frac{b}{2a}$=1可对②进行判断;利用抛物线的对称性可得抛物线与x轴的另一个交点在(2,0)和(3,0)之间,则x=3时,y<0,于是可对③进行判断;由于x=-1时,y<0,即a-b+c<0;x=1时,y>0,即a+b+c>0,(a-b+c)(a+b+c)<0,则利用平方差公式展开后可对④进行判断,最后利用概率公式计算所抽卡片上的结论正确的概率.
解答 解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=1,
∴b=-2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,所以①错误;
∵b=-2a,
∴2a+b=0,所以②正确;
∵抛物线与x轴的一个交点在(-1,0)和(0,0)之间,
∴抛物线与x轴的另一个交点在(2,0)和(3,0)之间,
∴当x=3时,y<0,
∴9a+3b+c<0,所以③正确;
∵x=-1时,y<0,即a-b+c<0;x=1时,y>0,即a+b+c>0,
∴(a-b+c)(a+b+c)<0,即[(a+c)-b][(a+c)+b]<0,
∴(a+c)2-b2<0,所以④错误.
∴小东同学从中随机抽取一张,所抽卡片上的结论正确的概率=$\frac{2}{4}$=$\frac{1}{2}$.
故答案为$\frac{1}{2}$.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);△决定抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了概率公式.

 阅读快车系列答案
阅读快车系列答案| A. | 任何一个三角形都有且只有一个外接圆 | |
| B. | 任何一组数据的中位数和平均数都不会相等 | |
| C. | 对角线相等且互相垂直的四边形是矩形 | |
| D. | 位似变换不改变图形的形状和大小 |
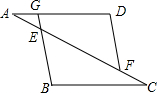 如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )| A. | $\frac{AG}{AD}=\frac{AE}{AF}$ | B. | $\frac{AG}{AD}=\frac{EG}{DF}$ | C. | $\frac{AE}{AC}=\frac{AG}{AD}$ | D. | $\frac{AD}{BC}=\frac{DF}{BE}$ |
| 级别 | 月用水量 | 水价 |
| 第1级 | 20吨以下(含20吨) | 1.6元/吨 |
| 第2级 | 20吨-30吨(含30吨) | 超过20吨部分按2.4元/吨 |
| 第3级 | 30吨以上 | 超过30吨部分按4.8元/吨 |
(2)若张红家6月份缴交水费44元,则该月用水量为25吨;
(3)若张红家7月份用水量为a吨(a>30),请计算该月需缴交水费多少元?(用含a的代数式表示)
| A. | 9a2-4b2=(3a-2b)2 | B. | -3ab2+6ab=-3ab(b+2) | ||
| C. | $\frac{1}{2}$a2-ab+$\frac{1}{2}$b2=$\frac{1}{2}$(a-b)2 | D. | -a2-b2=-(a+b)(a-b) |
| 阶梯 | 电量 | 电价 |
| 一档 | 0-180度 | 0.6元/度 |
| 二档 | 181-400度 | 二档电价 |
| 三档 | 401度及以上 | 三档电价 |