题目内容
8．先化简，再求值（$\frac{3x}{x-2}$-$\frac{x}{x+2}$）÷$\frac{x}{{x}^{2}-4}$．其中x是-2、-1、0、2中的一个．分析 先化简分式，再由分式有意义可得x=-1，代入求解即可．
解答 解：（$\frac{3x}{x-2}$-$\frac{x}{x+2}$）÷$\frac{x}{{x}^{2}-4}$
=[$\frac{3x（x+2）}{（x+2）（x-2）}$-$\frac{x（x-2）}{（x+2）（x-2）}$]×$\frac{（x+2）（x-2）}{x}$，
=2x+8，
由分式有意义可得x≠-2、0或2，
当x=-1时，原式=2×（-1）+8=6．
点评 本题主要考查了分式的化简求值，解题的关键是正确化简分式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，其对称轴为直线x=1．小夏同学给出了如下四个结论：①abc＞0；②2a+b=0；③9a+3b+c＜0；④（a+c）2＞b2，并把它们分别写在四张相同卡片上，将卡洗匀后背面朝上，小东同学从中随机抽取一张，所抽卡片上的结论正确的概率为$\frac{1}{2}$．
3．
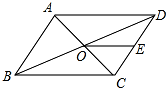如图，平行四边形ABCD的周长为36，对角线AC、BD相较于点O，点E是CD的中点，BD=12，则△DOE的周长为（ ）
如图，平行四边形ABCD的周长为36，对角线AC、BD相较于点O，点E是CD的中点，BD=12，则△DOE的周长为（ ）| A． | 12 | B． | 15 | C． | 18 | D． | 21 |
20．已知两点A（5，6）、B（7，2），先将线段AB向左平移一个单位，再以原点O为位似中心，在第一象限内将其缩小为原来的$\frac{1}{2}$得到线段CD，则点A的对应点C的坐标为（ ）
| A． | （2，3） | B． | （3，1） | C． | （2，1） | D． | （3，3） |
如图，E、F分别是?ABCD的一组对边AD、BC的中点，连接AF、BE相交于点G，EC、DF交于点H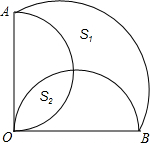
如图，扇形OAB的圆心角是90°，分别以OA、OB为直径在扇形内作圆，则S1、S2两部分图形面积的大小关系是什么？