题目内容
甲乙两人玩摸球游戏:一个不透明的袋子中装有相同大小的3个球,球上分别标有数字1,2,3.首先,甲从中随机摸出一个球,然后,乙从剩下的球中随机摸出一个球,比较球上的数字,较大的获胜.
(1)求甲摸到标有数字3的球的概率;
(2)这个游戏公平吗?请说明理由.
(1)求甲摸到标有数字3的球的概率;
(2)这个游戏公平吗?请说明理由.
考点:游戏公平性,概率公式
专题:
分析:(1)直接根据概率公式求出该事件的概率即可.
(2)游戏是否公平,求出游戏双方获胜的概率,比较是否相等即可
(2)游戏是否公平,求出游戏双方获胜的概率,比较是否相等即可
解答:
解:(1)∵袋子中装有相同大小的3个球,球上分别标有数字1,2,3,
∴甲摸到标有数字3的球的概率为
;
(2)解:游戏公平,理由如下:
列举所有可能:
由表可知甲获胜的概率=
,乙获胜的概率=
,
所以游戏是公平的.
∴甲摸到标有数字3的球的概率为
| 1 |
| 3 |
(2)解:游戏公平,理由如下:
列举所有可能:
| 甲 乙 | 1 | 2 | 3 |
| 1 | 3 | 1 | |
| 2 | 3 | 2 | |
| 3 | 2 | 1 |
| 1 |
| 2 |
| 1 |
| 2 |
所以游戏是公平的.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
若
=
,则
=( )
| a |
| b |
| 3 |
| 4 |
| b |
| a-b |
| A、-4 | ||
| B、4 | ||
C、-
| ||
D、
|
下列式子中正确的是( )
| A、4×4×4=3×4 | ||||||||
| B、53=35 | ||||||||
| C、(-3)×(-3)×(-3)×(-3)=34 | ||||||||
D、(-
|
若点A(x,3)与点B(2,y)关于x轴对称,则( )
| A、x=-2,y=-3 |
| B、x=2,y=-3 |
| C、x=-2,y=3 |
| D、x=2,y=3 |
一盏台灯原价是100元,经连续两次升价后,价格变为121元.如果每次升价的百分率是一样的,那么设每次升价的百分率为x,那么x满足方程是( )
| A、100(1+x)2=121 |
| B、100(1-x)2=121 |
| C、100(1+2x)=121 |
| D、100(1-2x)=121 |
 如图是我市环北路改造后一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为( )
如图是我市环北路改造后一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为4m,水面最深地方的高度为1m,则该输水管的半径为( )| A、2m | B、2.5m |
| C、4m | D、5m |
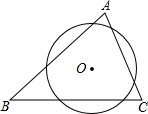 如图所示,在△ABC中,∠A=70°,⊙O截△ABC的三条边所得的弦长相等,则∠BOC的度数为( )
如图所示,在△ABC中,∠A=70°,⊙O截△ABC的三条边所得的弦长相等,则∠BOC的度数为( )| A、125° | B、130° |
| C、135° | D、160° |
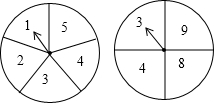 你喜欢转盘游戏吗?如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,
你喜欢转盘游戏吗?如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,