��Ŀ����
12��ijУ��֯�����꼶400��ѧ���������μ���չѵ�������֪��3��С�ͳ���1����ͳ�ÿ�ο�����ѧ��105�ˣ���1��С�ͳ���2����ͳ�ÿ�ο�����ѧ��110�ˣ���1��ÿ��С�ͳ���ÿ����ͳ�������������ѧ����
��2�����ƻ���С�ͳ�m������ͳ�n����һ�����꣬��ǡ��ÿ������������
��������Ƴ����е��������
����С�ͳ�ÿ�����250Ԫ����ͳ�ÿ�����350Ԫ����ѡ����ʡ�ߵ��������������������
���� ��1����ÿ��С�ͳ�����x�ˣ�ÿ����ͳ�����y�ˣ���������ɵõ�����ϵ��3��С�ͳ���������+1����ͳ���������=105�ˣ�1��С�ͳ���������+2����ͳ���������=110�ˣ����ݵ�����ϵ�г������飬�ٽ⼴�ɣ�
��2���ٸ�������ɵ�С�ͳ�m���˵�����+��ͳ�n���˵�����=400��Ȼ����������⼴�ɣ�
�ڸ��ݢ����÷�����С�ͳ�ÿ�����150Ԫ����ͳ�ÿ�����250Ԫ�ֱ�������ɣ�
��� ��1����1��С�ͳ�һ�ο���ѧ��x�ˣ�1����ͳ���������һ�ο���y��ѧ����
������ã�$\left\{\begin{array}{l}3x+y=105\\ x+2y=110\end{array}\right.$��
��ã�$\left\{\begin{array}{l}x=20\\ y=45\end{array}\right.$��
��1��С�ͳ���20�ˣ�1����ͳ���45�ˣ�
��2������С�ͳ�a������ͳ�b����������ã�
20a+45b=400��
��ÿ������ǡ�ö�������
��a��b��ֵ��Ϊ�Ǹ�������
��a��b��ȡ$\left\{\begin{array}{l}a=20\\ b=0\end{array}\right.$��$\left\{\begin{array}{l}a=11\\ b=4\end{array}\right.$��$\left\{\begin{array}{l}a=2\\ b=8\end{array}\right.$
�𣺹���3����������ٷֱ�����С��20�������������С��11�������4��������С��2�������8����
��3������1���Ϊ��250��20=5000��Ԫ����
����2���Ϊ��250��11+350��4=4150��Ԫ����
����3���Ϊ��250��2+350��8=3300��Ԫ����
�𣬷���3��ʡǮ����Ҫ3300Ԫ��
���� ������Ҫ�����˶�Ԫһ�η������Ӧ�ã��ؼ�����ȷ�������⣬�ҳ���Ŀ�еĵ�����ϵ���г���Ԫһ�η��̻��飮

 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�| A�� | $\sqrt{\frac{1}{3}}$ | B�� | $\sqrt{{m}^{2}+1}$ | C�� | $\sqrt{{a}^{3}}$��a��0�� | D�� | $\sqrt{8}$ |
| A�� | 3a3-2a2=0 | B�� | a3•a${\;}^{\frac{1}{3}}$=a | C�� | a3��a2=a | D�� | ��a2��${\;}^{\frac{1}{2}}$=a${\;}^{\frac{5}{2}}$ |
| A�� |  | B�� |  | ||
| C�� |  | D�� |  |
 ��֪����ͼ��OΪ��O��Բ�ģ���D�ڡ�O�ϣ�����AOC=110�㣬���ADC�Ķ���Ϊ��������
��֪����ͼ��OΪ��O��Բ�ģ���D�ڡ�O�ϣ�����AOC=110�㣬���ADC�Ķ���Ϊ��������| A�� | 55�� | B�� | 110�� | C�� | 125�� | D�� | 72.5�� |
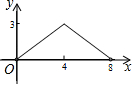
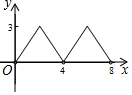
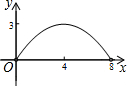
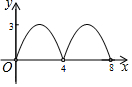
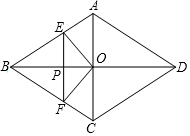 ��ͼ������ABCD�ĶԽ���AC��BD���ڵ�O��AC=6��BD=8������E�ӵ�B����������B-A-D������ABCD�ı����˶����˶�����Dֹͣ����F�ǵ�E����BD�ĶԳƵ㣬EF��BD�ڵ�P����BP=x����OEF�����Ϊy����y��x֮��ĺ���ͼ�����Ϊ��������
��ͼ������ABCD�ĶԽ���AC��BD���ڵ�O��AC=6��BD=8������E�ӵ�B����������B-A-D������ABCD�ı����˶����˶�����Dֹͣ����F�ǵ�E����BD�ĶԳƵ㣬EF��BD�ڵ�P����BP=x����OEF�����Ϊy����y��x֮��ĺ���ͼ�����Ϊ��������