题目内容
1.(1)计算:($\sqrt{3}$-2)0-(-1)2017+$\frac{1}{\sqrt{2}}$-sin45°;(2)化简:($\frac{x+1}{{x}^{2}-x}$-$\frac{x}{{x}^{2}-2x+1}$)÷$\frac{1}{x-1}$.
分析 (1)原式利用零指数幂法则,乘方的意义,以及特殊角的三角函数值计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=1+1+$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$=2;
(2)原式=[$\frac{{x}^{2}-1}{x(x-1)^{2}}$-$\frac{{x}^{2}}{x(x-1)^{2}}$]•(x-1)=-$\frac{1}{x(x-1)^{2}}$•(x-1)=-$\frac{1}{x(x-1)}$.
点评 此题考查了分式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠BAC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠BAC的正切值是( )
 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠BAC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠BAC的正切值是( )| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
16.以下计算正确的是( )
| A. | x8-x4=x4 | B. | (a4)2=a16 | C. | (a3b2)3=a4b5 | D. | a6÷a2=a4 |
 若关于x的不等式2x-m≥1的解集如图所示,则m=3.
若关于x的不等式2x-m≥1的解集如图所示,则m=3.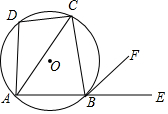 如图,四边形ABCD内接于⊙O,点E在AB的延长线上,BF∥AC,AB=BC,∠ADC=130°,则∠FBE=65°.
如图,四边形ABCD内接于⊙O,点E在AB的延长线上,BF∥AC,AB=BC,∠ADC=130°,则∠FBE=65°.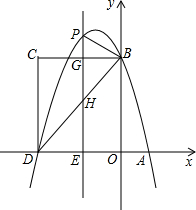 如图,在平面直角坐标系中,抛物线与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(-3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
如图,在平面直角坐标系中,抛物线与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(-3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.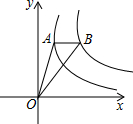 如图,在平面直角坐标系中,点A是函数y=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交函数y=$\frac{k}{x}$(x>0)的图象于点B,连结OA、OB.若△OAB的面积为$\frac{1}{2}$,则k的值为2.
如图,在平面直角坐标系中,点A是函数y=$\frac{1}{x}$(x>0)图象上一点,过点A作x轴的平行线,交函数y=$\frac{k}{x}$(x>0)的图象于点B,连结OA、OB.若△OAB的面积为$\frac{1}{2}$,则k的值为2.