题目内容

9．把下列多项式分解因式：
（1）m2-n2+2m-2n
（2）（x-1）（x-3）+1．

分析 （1）根据平方差公式将m2-n2变形为（m+n）（m-n），再提取公因数即可得出结论；
（2）将（x-1）（x-3）展开，再根据完全平方公式即可得出原式=（x-2）2．

解答 解：（1）原式=（m+n）（m-n）+2（m-n）=（m-n）（m+n+2）；
（2）原式=x2-4x+3+1=x2-4x+4=（x-2）2．

点评 本题考查了分解因式，熟练掌握分解因式的各种方法是解题的关键．

练习册系列答案
相关题目
19．如图1，正方形ABCD和正方形QMNP，M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．

（1）猜想：ME与MF的数量关系ME=MF；
（2）如图2，若将原题中的“正方形”改为“矩形”且AB：BC=1：2，其他条件不变，探索线段ME与线段MF的数量关系，并说明理由．
（3）如图3，若将原题中的“正方形”改为平行四边形，且∠M=∠B，AB：BC=m，其他条件不变，求出ME：MF的值．（直接写出答案）
20．解下列方程：
（1）（2x+1）2=9                        
（2）（3x-2）2=2-3x
（3）x2-4x+1=0                  
（4）（x-1）（x+2）=10．
17．某宾馆拥有客房100间，经营中发现：每天入住的客房数y（间）与房价x（元）（180≤x≤300）满足一次函数关系，部分对应值如下表：
x（元）180260280300
y（间）100605040
（1）求y与x之间的函数表达式；
（2）已知每间入住的客房，宾馆每日需支出各种费用100元；求宾馆当日利润w与房价x之间的函数关系式．（宾馆当日利润=当日房费收入-当日支出）
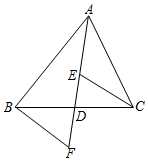4．如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，
连结BF，CE．下列说法：①△ABD和△ACD面积相等； ②∠BAD=∠CAD；
③△BDF≌△CDE；④BF∥CE；⑤CE=AE．其中正确的有①③④．（把你认为正确的序号都填上）
14．因式分解：
（1）3x-12x3
（2）m（x-y）+n（y-x）
1．当a=3，b=-1时，
（1）求代数式a2-b2和（a+b）（a-b）的值；
（2）猜想这两个代数式的值有何关系？
（3）根据（1）（2），你能用简便方法算出a=2016，b=2015时，a2-b2的值吗？
18．图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，点A和点B在小正方形的顶点上．请你在图1、图2中各画出一个直角三角形，使所画两直角三角形的形状不同（另一顶点为小正方形的顶点）．
19．如图所示，是一个外轮廓为长方形的机器零件平面示意图，根据图中标出的尺寸（单位：mm）请计算两圆孔中心A和B的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网