题目内容
13.已知矩形一边的长为5,另一边的长为4,则它的对角线的长为( )| A. | 3 | B. | $\sqrt{41}$ | C. | 4 | D. | 2$\sqrt{41}$ |
分析 由矩形的性质得出AC=BD,∠ABC=90°,由勾股定理求出AC即可.
解答 解: 如图所示:
如图所示:
∵四边形ABCD是矩形,
∴AC=BD,∠ABC=90°,
∵AB=4,BC=5,
∴BD=AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{5}^{2}}$=$\sqrt{41}$;
故选:B.
点评 本题考查了矩形的性质、勾股定理;熟练掌握矩形的性质,由勾股定理求出AC是解决问题的关键.

练习册系列答案
相关题目
4.下列对方程2x-3y=7变形正确的是( )
| A. | y=$\frac{7-2x}{3}$ | B. | y=$\frac{2x-7}{3}$ | C. | x=$\frac{3y-7}{2}$ | D. | x=$\frac{7-3y}{2}$ |
1.下列说法正确的是( )
| A. | 调查重庆市空气质量情况应该采用普查的方式 | |
| B. | A组数据方差$S_A^2=0.03$,B组数据方差$S_B^2=0.2$,则B组数据比A组数据稳定 | |
| C. | 重庆八中明年开运动会一定不会下雨 | |
| D. | 2,3,6,9,5这组数据的中位数是5 |
18.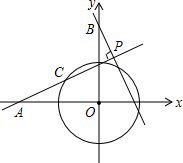 如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
 如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )| A. | $2\sqrt{2}$ | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | 2 | D. | $\frac{3}{2}$ |
5. 为响应我市“中国梦”•“株洲梦”主题教育活动,某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.孔明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
为响应我市“中国梦”•“株洲梦”主题教育活动,某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.孔明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
请你根据图表提供的信息,解答下列问题:
(1)完成表格和扇形统计图:a=5,b=20,n=144.
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
 为响应我市“中国梦”•“株洲梦”主题教育活动,某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.孔明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
为响应我市“中国梦”•“株洲梦”主题教育活动,某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.孔明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.| 等级 | 频数 | 频率 |
| 一等奖 | a | 0.1 |
| 二等奖 | 10 | 0.2 |
| 三等奖 | b | 0.4 |
| 优秀奖 | 15 | 0.3 |
(1)完成表格和扇形统计图:a=5,b=20,n=144.
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
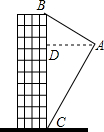 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为208米.(精确到1米,参考数据:$\sqrt{3}$≈1.73)
如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为208米.(精确到1米,参考数据:$\sqrt{3}$≈1.73) 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F. 如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°.
如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E,∠CBF=20°.