题目内容
4. 已知,如图,AD⊥BC,EF⊥BC,G为线段AB上的一个动点.
已知,如图,AD⊥BC,EF⊥BC,G为线段AB上的一个动点.(1)若BD=9,AB=41,当G点运动到DG⊥AB时,求DG的长;
(2)当G点运动到什么位置时,∠1=∠2,说明理由;
(3)在(2)的条件下,∠BAC=80°,∠GDC=150°,求∠B的度数.
分析 (1)直接利用勾股定理得出AD的长,再利用三角形面积求出答案;
(2)直接利用平行线的性质进而得出∠1=∠DAC,即可得出答案;
(3)利用平行线的性质以及结合邻补角的定义以及结合三角形内角和定理得出答案.
解答 解:(1)G点运动到DG⊥AB时,
∵BD=9,AB=41,∠ADB=90°,
∴AD=$\sqrt{4{1}^{2}-{9}^{2}}$=40,
∴BD•AD=DG•AB,
DG=$\frac{BD•AD}{AB}$=$\frac{9×40}{41}$=$\frac{360}{41}$;
(2)当DG∥AC时,∠1=∠2,
理由:∵AD⊥BC,EF⊥BC,
∴∠2=∠DAC,
∵DG∥AC,
∴∠1=∠DAC,
∴∠1=∠2;
(3)∵DG∥AC,∠BAC=80°,
∴∠BGD=80°,
∵∠GDC=150°,
∴∠BDG=30°,
∴∠B=70°.
点评 此题主要考查了平行线的判定与性质以及勾股定理和三角形内角和定理等知识,正确把握平行线的性质是解题关键.

练习册系列答案
相关题目
15.已知下列各式$\frac{x30%}{m}$,$\frac{a}{2}$,ah+2$\frac{2}{3}$x,3x+2,$\frac{1}{2}$x,a×2,其中不符合代数式书写规范的有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
13.已知等腰△ABC中,AB=AC,点D为BC边上一点,连接AD,若△ACD和△ABD都是等腰三角形,则∠ACB的度数为( )
| A. | 36° | B. | 45° | C. | 36°或45° | D. | 36°或45°或72° |
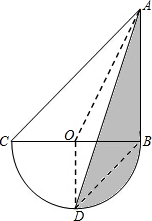 如图,三角形ABC是等腰直角三角形,D是圆周的中点,BC是半圆的直径,已知AB=BC=10厘米,那么阴影部分面积是多少?
如图,三角形ABC是等腰直角三角形,D是圆周的中点,BC是半圆的直径,已知AB=BC=10厘米,那么阴影部分面积是多少?
