题目内容
1.观察下面的一组分式:$\frac{{b}^{2}}{a}$,-$\frac{{b}^{5}}{{a}^{2}}$,$\frac{{b}^{8}}{{a}^{3}}$,-$\frac{{b}^{11}}{{a}^{4}}$,$\frac{{b}^{14}}{{a}^{5}}$…(1)求第10个分式是多少?
(2)列出第n个分式.
分析 (1)观察分子的变化:b2、b5、b8…b3n-1.观察分母,a1、a2、a3…an.观察分式的符号,奇数项为正数,偶数项为负数;
(2)根据(1)的推断过程得到通式.
解答 解:(1)∵$\frac{{b}^{2}}{a}$=(-1)1+1$\frac{{b}^{3×1-1}}{{a}^{1}}$,
-$\frac{{b}^{5}}{{a}^{2}}$=(-1)2+1$\frac{{b}^{3×2-1}}{{a}^{2}}$,
$\frac{{b}^{8}}{{a}^{3}}$=(-1)3+1$\frac{{b}^{3×3-1}}{{a}^{3}}$,
-$\frac{{b}^{11}}{{a}^{4}}$=(-1)4+1$\frac{{b}^{3×4-1}}{{a}^{4}}$,
…
∴第10个分式是:-$\frac{{b}^{3×10-1}}{{a}^{10}}$=-$\frac{{b}^{29}}{{a}^{10}}$.
(2)由(1)得到第n个分式为:=(-1)n+1$\frac{{b}^{3n-1}}{{a}^{n}}$.
点评 本题考查了分式的定义.解答此类规律题时,要对分子、分母的变化规律作出总结,也不要漏掉分式本身符号变化规律的总结.

练习册系列答案
相关题目
 看图回答问题:
看图回答问题: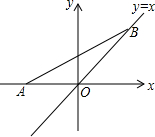 如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标.
如图,点A的坐标为(-$\sqrt{2}$,0),点B在直线y=x上运动,当线段AB最短时,求点B的坐标. 如图,正六边形ABCDEF的边长为2,则对角线AC=2$\sqrt{3}$.
如图,正六边形ABCDEF的边长为2,则对角线AC=2$\sqrt{3}$.