题目内容
20.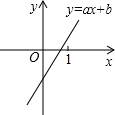 一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )| A. | 2a | B. | -2a | C. | 2b | D. | -2b |
分析 根据一次函数图象与系数的关系结合当x=1时y>0,即可得出a>0、b<0、a+b>0,进而可得出a-b>0,依此即可得出$\sqrt{{{(a-b)}^2}}$-|a+b|=(a-b)-(a+b)=-2b,此题得解.
解答 解:观察函数图象可知:a>0,b<0,a+b>0,
∴a-b>0,
∴$\sqrt{{{(a-b)}^2}}$-|a+b|=(a-b)-(a+b)=-2b.
故选D.
点评 本题考查了一次函数图象与系数的关系以及二次根式的化简求值,观察函数图象找出a>0、b<0、a+b>0是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{a}$+$\sqrt{2a}$=$\sqrt{3a}$ | B. | (ab3)2=a2b5 | C. | 2a+3a=6a | D. | a•a3=a4 |

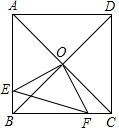 如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于5.
如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于5.