题目内容
12.化简求值:$\frac{m+\sqrt{mn}}{\sqrt{mn}+n}+\frac{\sqrt{mn}-n}{m-\sqrt{mn}}$,其中m=2+$\sqrt{3}$,n=2-$\sqrt{3}$.分析 把m=2+$\sqrt{3}$,n=2-$\sqrt{3}$代入代数式求得即可.
解答 解:∵m=2+$\sqrt{3}$,n=2-$\sqrt{3}$,
∴mn=4-3=1,
∴原式=$\frac{2+\sqrt{3}+1}{1+2-\sqrt{3}}$+$\frac{1-2+\sqrt{3}}{2+\sqrt{3}-1}$=$\frac{3+\sqrt{3}}{3-\sqrt{3}}$+$\frac{\sqrt{3}-1}{\sqrt{3}+1}$=$\frac{12+2\sqrt{3}}{6}$+$\frac{4-2\sqrt{3}}{2}$=$\frac{6+\sqrt{3}}{3}$+$\frac{6-3\sqrt{3}}{3}$=$\frac{12-2\sqrt{3}}{3}$=4-$\frac{2\sqrt{3}}{3}$.
点评 此题主要考查了二次根式的化简求值,二次根式运算时注意乘法公式的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.某班组织了一次读书活动,统计了16名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这16名同学一周内累计读书时间的中位数是9.
| 一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
| 人数(个) | 1 | 7 | 5 | 3 |
20.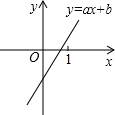 一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
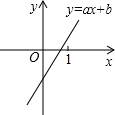 一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )
一次函数y=ax+b在直角坐标系中的图象如图所示,则化简$\sqrt{{{(a-b)}^2}}$-|a+b|的结果是( )| A. | 2a | B. | -2a | C. | 2b | D. | -2b |
7.下列计算中,正确的是( )
| A. | 2a+3a=5a | B. | a3•a2=a6 | C. | a3÷a2=1 | D. | (-a)3=a3 |
17.-$\sqrt{17}$+1的小数部分是( )
| A. | -$\sqrt{17}$+5 | B. | -$\sqrt{17}$+4 | C. | -$\sqrt{17}$-3 | D. | $\sqrt{17}$-4 |
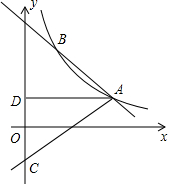 如图,反比例函数y=$\frac{k}{x}$(x>0)图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
如图,反比例函数y=$\frac{k}{x}$(x>0)图象经过点A(2$\sqrt{3}$,1),直线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.