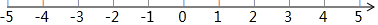题目内容
9．某工厂生产的某种产品按质量分为10个档次，第1档次（最低档次）的产品一天能生产76件，每件利润10元．每提高一个档次，每件利润增加2元．（1）每件利润为14元时，此产品质量在第几档次？
（2）由于生产工序不同，产品每提高1个档次，一天产量减少4件．若生产第x档的产品一天的总利润为y元（其中x为正整数，且1≤x≤10），求出y关于x的函数关系式；若生产某档次产品一天的总利润为1080元，该工程生产的是第几档次的产品？
分析 （1）由每提高一个档次，每件利润增加2元，14-10=4，需要提高2个档次，由此即可解决问题．
（2）根据一天的利润=生产的件数×每件的利润，即可求出y与x的关系，再列出方程即可解决问题．
解答 解：（1）每件利润为14元时，此产品质量在第3档次．
（2）由题意y=[10+2（x-1）][76-4（x-1）]=-8x2+128x+640．（1≤x≤10）．
当y=1080时，-8x2+128x+640=1080，
解得x=5或11（舍弃）．
答：工程生产的是第5档次的产品时，一天的总利润为1080元．
点评 本题考查二次函数的应用、一元二次方程的解法等知识，解题的关键是学会把问题转化为方程解决，属于中考常考题型．
练习册系列答案
相关题目
实数a、b在数轴上的位置如图所示，化简：$\sqrt{（a-1）^{2}}$-|2-b|+$\sqrt{（b-a）^{2}}$．
20．下列分式是最简分式的是（ ）
| A． | $\frac{x-1}{{x}^{2}-x}$ | B． | $\frac{x-1}{x+1}$ | C． | $\frac{x-1}{{x}^{2}-1}$ | D． | $\frac{4}{4x}$ |
17．一个正整数的算术平方根为a，则比这个正整数大3的数的算术平方根是（ ）
| A． | a+3 | B． | a+$\sqrt{3}$ | C． | $\sqrt{{a}^{2}+3}$ | D． | $\sqrt{a+3}$ |
14．
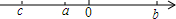已知有理数a，b，c在数轴上对应点的位置如图所示，化简：|b-c|-2|c+a|-3|a-b|=（ ）
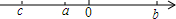已知有理数a，b，c在数轴上对应点的位置如图所示，化简：|b-c|-2|c+a|-3|a-b|=（ ）| A． | -5a+4b-3c | B． | 5a-2b+c | C． | 5a-2b-3c | D． | a-2b-3c |
