题目内容
12.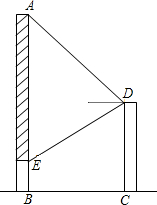 如图,为响应泰安市人民政府“形象重于生命”的号召,在甲建筑物上从A点到E点挂一长为30米的宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,求底部不能直接到达的甲乙两建筑物之间的水平距离BC.
如图,为响应泰安市人民政府“形象重于生命”的号召,在甲建筑物上从A点到E点挂一长为30米的宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,求底部不能直接到达的甲乙两建筑物之间的水平距离BC.
分析 根据∠ADF和∠BDF可以求得AF与DF、BF与DF的关系,即可求得DF的值,即可解题.
解答  解:过D点作DF⊥AB于F,
解:过D点作DF⊥AB于F,
∵AB⊥BC,DC⊥BC,∴∠ABC=∠BCD=∠DFB=90°,
∴BCDF是矩形,∴CD=BF,DF=BC,
∵∠ADF=45°,∴AF=DFtan45°=DF,
∵∠EDF=30°,∴EF=DFtan30°=$\frac{\sqrt{3}}{3}$DF,
∴AE=AF+EF,则DF+$\frac{\sqrt{3}}{3}$DF=30,
∴DF=(45-15$\sqrt{3}$)米
即BC=(45-15$\sqrt{3}$) 米.
点评 本题考查了特殊角的三角函数值,三角函数在直角三角形中的运用,本题中根据DF求AF、EF是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
3.若4a-9与3a-5互为相反数,则a的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | 0 |
20.下列分式是最简分式的是( )
| A. | $\frac{x-1}{{x}^{2}-x}$ | B. | $\frac{x-1}{x+1}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{4}{4x}$ |
7.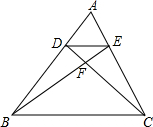 如图,在△ABC中,DE∥BC,BE和CD相交于点F,且S△EFC=3S△EFD,则S△ADE:S△ABC的值为( )
如图,在△ABC中,DE∥BC,BE和CD相交于点F,且S△EFC=3S△EFD,则S△ADE:S△ABC的值为( )
 如图,在△ABC中,DE∥BC,BE和CD相交于点F,且S△EFC=3S△EFD,则S△ADE:S△ABC的值为( )
如图,在△ABC中,DE∥BC,BE和CD相交于点F,且S△EFC=3S△EFD,则S△ADE:S△ABC的值为( )| A. | 1:3 | B. | 1:8 | C. | 1:9 | D. | 1:4 |
17.一个正整数的算术平方根为a,则比这个正整数大3的数的算术平方根是( )
| A. | a+3 | B. | a+$\sqrt{3}$ | C. | $\sqrt{{a}^{2}+3}$ | D. | $\sqrt{a+3}$ |
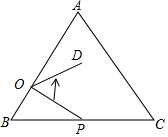 在等边△ABC中,AC=9,点O在AB上,且BO=3,点P是BC上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在AC边上,则BP的长是6.
在等边△ABC中,AC=9,点O在AB上,且BO=3,点P是BC上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在AC边上,则BP的长是6.