题目内容
16. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠-1),其中正确的结论有①③④.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠-1),其中正确的结论有①③④.
分析 由函数的图象可以得到a、b、c的符号,再根据图象和灵活的变化得到题目中的结论是否正确.
解答 解:因为函数图象与x轴两个交点,故b2-4ac>0,即4ac-b2<0,故①正确;
因为$-\frac{b}{2a}=-1$,所以b=2a,因为图象与y轴交于正半轴,故c>0,故4a-2b+c>0,即4a+c>2b,故②错误;
由图象可知,x=1时,a+b+c<0,则2a+2b+2c<0,即3b+2c<0,故③正确;
由图象可知:x=-1时,函数有最大值a-b+c,令x=m(m≠-1),则am2-bm+c<a-b+c,则am2-bm+b<a,即m(am+b)+b<a(m≠-1),④正确.
故答案为:①③④.
点评 本题考查了二次函数图象与系数之间的关系,学生对式子的灵活变化.

练习册系列答案
相关题目
7.已知动点P以2厘米/秒的速度沿图(a)的边框 BCDEFA 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图(b)所示.若 AB=6厘米,则下列答案正确的是( )
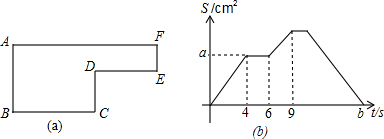

| A. | 图(a)中的BC长是4cm | B. | 图(b)中的a是12 | ||
| C. | 图(a)中的图形面积是60cm2 | D. | 图(b)中的b是19 |
6.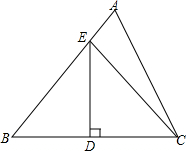 如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )
如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )
 如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )
如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )| A. | 18 | B. | 20 | C. | 26 | D. | 28 |
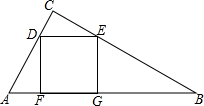 如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.
如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.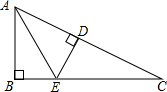 如图,在△ABC中,∠B=90°,E为BC上一点,ED⊥AC于点D,AB=AD,∠C=20°,求∠AEB的度数.
如图,在△ABC中,∠B=90°,E为BC上一点,ED⊥AC于点D,AB=AD,∠C=20°,求∠AEB的度数. 如图,已知点D、E、F分别在△ABC的边AB、AC、BC上,DE∥BC、DF∥AC,AE=6,EC=8,求BF:FC的值.
如图,已知点D、E、F分别在△ABC的边AB、AC、BC上,DE∥BC、DF∥AC,AE=6,EC=8,求BF:FC的值.