题目内容
已知△ABC，求作一点P，使P到三角形三边的距离相等，则点P是（ ）
| A、三边中垂线的交点 |
| B、三边的高线的交点 |
| C、三边中线的交点 |
| D、三个内角的角平分线的交点 |
考点：角平分线的性质
专题：
分析：到三角形三边都相等的点应该在三角形三个内角的角平分线上，可得出答案．
解答：解：
∵P到AB、AC两边的距离相等，
∴点P在∠BAC的平分线上，
同理可得点P在∠ABC、∠ACB的平分线上，
∴点P为三个内角的角平分线的交点，
故选D．
∵P到AB、AC两边的距离相等，
∴点P在∠BAC的平分线上，
同理可得点P在∠ABC、∠ACB的平分线上，
∴点P为三个内角的角平分线的交点，
故选D．
点评：本题主要考查角平分线的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．
练习册系列答案
相关题目
已知：如图，线段a、b、c．
如图，在△ABC中，∠C=90°，∠A=15°，∠DBC=60°，BC=4，则AD=
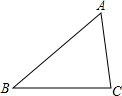有三个社区A、B、C位置如图所示，为了检测三个社区的登革热情况，现需要设立检测点0，要求该点到三个社区距离相等，则点0应为△ABC的三条（ ）| A、高的交点 |
| B、角平分线的交点 |
| C、中线的交点 |
| D、垂直平分线的交点 |
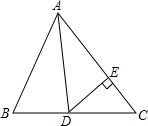如图所示，在△ABC中，已知AD是角平分线，∠B=66°，∠C=54°．
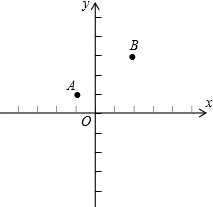在直角坐标系中，有两点A（-1，1），B（2，3）