题目内容
13．已知a，b是等腰三角形的两边，且满足a2+$\sqrt{b-4}$=16a-64．求三角形的周长．分析 根据a2+$\sqrt{b-4}$=16a-64可得（a-8）2+$\sqrt{b-4}$=0，即a=8、b=4，根据三角形三边关系可求出周长．
解答 解：由a2+$\sqrt{b-4}$=16a-64，可得：
a2-16a+64+$\sqrt{b-4}$=0，即（a-8）2+$\sqrt{b-4}$=0，
∴a=8，b=4，
当等腰三角形的腰长为4时，此时三角形三边为4，4，8，不能构成三角形；
当等腰三角形的腰长为8时，此时等腰三角形三边长为8，8，4，
则三角形的周长为20．
点评 本题主要考查配方法的应用、非负数性质、等腰三角形性质及三角形三边关系，配方得到非负数和为0是解题的前提和关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
分别在直角坐标系中描出点（1）（0，0），（5，4），（3，0），（5，1）（5，-1），（3，0），（4，-2），（0，0）；按描点的顺序连线．
如图，在Rt△ABC中，∠ABC=90°，AB=8，BC=6，点D为AC边上的动点，点D从点C出发，沿边CA向点A运动，当运动到点A时停止，若设点D运动的时间为t秒．点D运动的速度为每秒1个单位长度．
8．
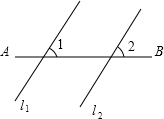如图，将直线l1沿AB的方向平移得到l2，若∠1=40°，则∠2=（ ）
如图，将直线l1沿AB的方向平移得到l2，若∠1=40°，则∠2=（ ）| A． | 40° | B． | 50° | C． | 90° | D． | 140° |