题目内容
4.某商场打算在年前用30000元购进一批彩灯进行销售,由于进货厂家促销,实际可以以8折的价格购进这批彩灯,结果可以比计划多购进了100盏彩灯.(1)该商场购进这种彩灯的实际进价为多少元?
(2)该商场打算在实际进价的基础上,每盏灯加价50%的销售,但可能会面临滞销,因此将有20%的彩灯需要降价,以5折出售,该商场要想获利不低于15000元,应至少在购进这种彩灯多少盏?
分析 (1)设该商场实际购进每盏彩灯为x元,则实际进价为0.8x元,根据实际比计划多购进100盏彩灯,列方程求解;
(2)设再购进彩灯a盏,根据利润=售价-进价和货栈要想获得利润不低于15000元列出不等式并解答.
解答 解:(1)设该商场实际购进每盏彩灯为x元,则实际进价为0.8x元,
依题意得:$\frac{30000}{0.8x}$=$\frac{30000}{x}$+100,
解得x=75,
经检验x=75是所列方程的根,
则0.8x=0.8×75=60(元).
答:该货栈实际购进每盏彩灯为60元;
(2)设再购进彩灯a盏,
由(1)知,实际购进30000÷60=500(盏),
依题意得:(500+a)(1-20%)×60×50%+(500+a)×20%×[60×(1+50%)×0.5-60]≥15000,
解得a≥$\frac{1500}{7}$.
因为a取正整数,
所以a=215.
答:至少再购进彩灯215盏.
点评 本题考查了分式方程和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程和不等式求解,注意检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.今年参加菏泽市初中毕业学业水平考试的考生约有71000人,请将数字71000用科学记数法表示为( )
| A. | ×103 | B. | 7.1×104 | C. | 0.71×105 | D. | 71×103 |
17.为了了解某班学生每天使用零花钱的情况,班主任随机调查了15名同学,调查的结果如下表:
对于表中数据,下列说法正确的是( )
| 人数 | 1 | 3 | 5 | 4 | 2 |
| 每天零花钱(元) | 0 | 1 | 3 | 4 | 5 |
| A. | 中位数是3元 | B. | 平均数是2.5元 | C. | 方差是4 | D. | 众数是5元 |
16.考虑下面两种移动电话计费方式:
用函数方法解答何时两种计费方式费用相等.
| 方式一 | 方式二 | |
| 月租费/(元/月) | 30 | 0 |
| 本地通话费/(元/min) | 0.30 | 0.40 |
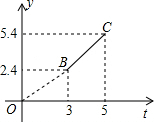 图中折线OBC表示从甲地向乙地打长途电话所付的电话费y(元)与通话时间x(分钟)之间的关系图象.
图中折线OBC表示从甲地向乙地打长途电话所付的电话费y(元)与通话时间x(分钟)之间的关系图象.