题目内容
A，B两点间有一条传输速度为每分钟5米的传送带，由A点向B点传送货物．一只蚂蚁不小心爬到了传送带上，它以每分钟1.5米的速度从A点爬向B点，3分钟后，蚂蚁爬到了B点，你能求出A，B两点间的距离吗?
19.5米．
【解析】试题分析：蚂蚁的爬行速度是1.5米/分，传送带的传送速度为5米/分，并且传送带的传送方向与蚂蚁的爬行方向相同，所以蚂蚁从A点向B运动的速度是(5＋1.5)米/分，运动的时间是3分，根据路程＝速度×时间即可得出A，B两点间的距离．
试题解析：
【解析】
蚂蚁运动的速度是5＋1.5＝6.5米/分，
所以A，B两点间的距离是：6.5×3＝19.5米．
练习册系列答案
相关题目
如图所示，四边形ABCD中，AE、AF分别是BC、CD的垂直平分线，∠EAF＝80°，∠CBD＝30°，则∠ADC的度数为( )
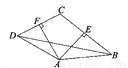
A. 45° B. 60°
C. 80° D. 100°
B
【解析】连接AC，
∵AE、AF分别是BC、CD的垂直平分线，
∴AB=AC=AD，
∵AF⊥DC，AE⊥BC，
∴∠CAF=∠DAF，∠CAE=∠BAE．
∴∠DAB=2∠EAF=160°，
∴∠ABD=（180°-160°）÷2=10°，
∴∠ABC=∠ACB=30°+10°=40°；
在四边形AECF中，
∠FCE=360°-9... 如图，将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△A′B′C′，使点B′与C重合，连接A′B，则tan∠A′BC′＝________.
【解析】过A′作出A′D⊥BC′，垂足为D，
在等腰直角三角形A′B′C′中，则A′D是底边上的中线，
∴B′C′=2 A′D，
∵BC=B′C′，
∴BD=BC+B′D=3 A′D，
∴ tan∠A′BC′=，
故答案为： . 分解因式：2ab2－6a2b＋ab;
ab(2b－6a＋1)
【解析】试题分析：根据提公因式法分解因式，先确定公因式ab，再提取公因式即可.
试题解析：2ab2－6a2b＋ab = ab(2b－6a＋1). －9a2b＋3ac2－6abc各项的公因式是_______；
－3a
【解析】根据提公因式法因式分解，可知其是首项为“﹣”的多项式，因此可知其公因式为-3a.
故答案为：-3a. 如图所示，将Rt△ABC沿直角边AB的方向向右平移2个单位得到△DEF，如果AB＝4，∠ABC＝90°，且△ABC的面积为6，试求图中阴影部分的面积．
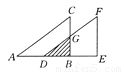
【解析】试题分析：根据△ABC的面积求出BC的长，根据平移的性质计算出BD的长，再根据平行线分线段成比例定理求出BG的长，最后利用三角形的面积公式计算即可得出答案．
试题解析：
【解析】
因为S△ABC＝AB·BC＝6，
所以BC＝3，
由平移可知AD＝2，BC∥EF，
所以BD＝AB－AD＝4－2＝2，
所以＝，
所以BG＝BC＝，
所以S△BD... 一个三角形最初的一个顶点为A，把它先向下平移4个单位长度时的位置记为B，再向左平移3个单位长度时的位置记为C，则由A，B，C三点所组成的三角形的周长为 ( )
A. 7 B. 14 C. 12 D. 15
C
【解析】试题分析：如图所示：
AB＝4，BC＝3，
则AC＝5，
故由A，B，C三点所组成的三角形的周长为：3＋4＋5＝12．
故选C． 如图所示，H是△ABC的高AD，BE的交点，且DH=DC，则下列结论：①BD=AD；②BC=AC；③BH=AC；④CE=CD中正确的有（ ）
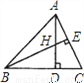
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】【解析】
①∵BE⊥AC，AD⊥BC，∴∠AEH=∠ADB=90°．
∵∠HBD+∠BHD=90°，∠EAH+∠AHE=90°，∠BHD=∠AHE，∴∠HBD=∠EAH．
∵DH=DC，∴△BDH≌△ADC（AAS），∴BD=AD，BH=AC；
②∵BC=AC，∴∠BAC=∠ABC．
由①知，在Rt△ABD中，∵BD=AD，∴∠ABC=45°，∴∠BAC... 下列图形经过平移后恰好可以与原图形组合成一个长方形的是（ ）
A. 三角形 B. 正方形 C. 梯形 D. 都有可能
B
【解析】试题解析：正方形能够通过平移而得到的新图形和原图形组合成一个长方形.
故选B.