题目内容
12.已知一扇形的弧长是4π,半径为3,那么这个扇形的面积是6π.分析 直接根据扇形的面积公式S扇形=$\frac{1}{2}$lR进行计算.
解答 解:根据扇形的面积公式,得
S扇形=$\frac{1}{2}$lR=$\frac{1}{2}$×4π×3=6π.
故答案为:6π.
点评 本题考查了扇形面积的计算,比较简单,解答本题的关键是熟练掌握扇形面积的计算公式.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
3. 如图,AB为斜坡,D是斜坡AB上一点,斜坡AB的坡度为i,坡角为α,AC⊥BM于点C,下列式子:①i=AC:AB;②i=(AC-DE):EC;③i=tanα=$\frac{DE}{BE}$;④AC=i•BC,其中正确的有( )
如图,AB为斜坡,D是斜坡AB上一点,斜坡AB的坡度为i,坡角为α,AC⊥BM于点C,下列式子:①i=AC:AB;②i=(AC-DE):EC;③i=tanα=$\frac{DE}{BE}$;④AC=i•BC,其中正确的有( )
 如图,AB为斜坡,D是斜坡AB上一点,斜坡AB的坡度为i,坡角为α,AC⊥BM于点C,下列式子:①i=AC:AB;②i=(AC-DE):EC;③i=tanα=$\frac{DE}{BE}$;④AC=i•BC,其中正确的有( )
如图,AB为斜坡,D是斜坡AB上一点,斜坡AB的坡度为i,坡角为α,AC⊥BM于点C,下列式子:①i=AC:AB;②i=(AC-DE):EC;③i=tanα=$\frac{DE}{BE}$;④AC=i•BC,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 如图,AB是⊙O的一条直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P的位置是否发生变化?并说明理由.
如图,AB是⊙O的一条直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P的位置是否发生变化?并说明理由.
 如图,AB是⊙O的一条直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P的位置是否发生变化?并说明理由.
如图,AB是⊙O的一条直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P的位置是否发生变化?并说明理由.
17.小华和小刚兄弟两个同时从家去同一所学校上学,速度都是每分钟走50米.小华从家到学校走直线用了10分钟,而小刚从家出发先去找小明再到学校(均走直线),小刚到小明家用了6分钟,小明家到学校用了8分钟,小刚上学走了个( )
| A. | 锐角弯 | B. | 钝角弯 | C. | 直角弯 | D. | 不能确定 |
1.能判定△ABC∽△A′B′C′的条件是( )
| A. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′ | B. | $\frac{AB}{A′C′}$=$\frac{A′B′}{AC}$,∠B=∠B′ | ||
| C. | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠A=∠A′ | D. | $\frac{AB}{A′B′}$=$\frac{AC}{B′C′}$,∠A=∠A′ |
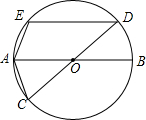 如图,AB,CD是⊙O的直径,弦DE∥AB,则AC与AE的大小关系是AC=AE.
如图,AB,CD是⊙O的直径,弦DE∥AB,则AC与AE的大小关系是AC=AE. 如图,已知点M是反比例函数y=-$\frac{6}{x}$的图象上任意一点,过点M分别作x轴、y轴的垂线,垂足依次为P,Q,那么四边形OQMP的面积为6.
如图,已知点M是反比例函数y=-$\frac{6}{x}$的图象上任意一点,过点M分别作x轴、y轴的垂线,垂足依次为P,Q,那么四边形OQMP的面积为6.