题目内容
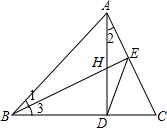 如图,在△ABC 中,高AD和高BE交于H点,且∠1=∠2=22.5°,下列结论中:①∠2=∠3;②BD=AD;③BD+DH=AB,其中结论正确的是( )
如图,在△ABC 中,高AD和高BE交于H点,且∠1=∠2=22.5°,下列结论中:①∠2=∠3;②BD=AD;③BD+DH=AB,其中结论正确的是( )| A、0个 | B、1个 | C、2个 | D、3个 |
考点:全等三角形的判定与性质
专题:
分析:根据三角形内角和定理求出∠2=∠3=∠1=22.5°,求出∠ABD=45°,推出AD=BD,过H作HM⊥AB于M,根据角平分线性质得出HM=DH,求出AM=HM,求出BM=BD即可.
解答:解:∵在△ABC 中,高AD和高BE交于H点,
∴∠HDB=∠CDA=∠AEH=90°,
∵∠AHE=∠BHD,
∴根据三角形内角和定理得:∠2=∠3,
∵∠1=∠2=22.5°,
∴∠3=22.5°,
∴∠ABD=45°,
∴∠BAD=45°,
∴∠ABD=∠BAD,
∴BD=AD,
过H作HM⊥AB于M,
则∠AMH=90°,
∵∠BAD=45°,
∴∠AHM=45°=∠BAD,
∴HM=AM,
∵∠1=∠3=22.5°,HD⊥BC,HM⊥AB,
∴DH=HM=AM,
在△BMH和△BHD中
∴△BMH≌△BHD,
∴BM=BD,
∴AB=BM+AM=BD+DH,∴①②③正确;
故选D.
∴∠HDB=∠CDA=∠AEH=90°,
∵∠AHE=∠BHD,
∴根据三角形内角和定理得:∠2=∠3,
∵∠1=∠2=22.5°,
∴∠3=22.5°,
∴∠ABD=45°,
∴∠BAD=45°,
∴∠ABD=∠BAD,
∴BD=AD,

过H作HM⊥AB于M,
则∠AMH=90°,
∵∠BAD=45°,
∴∠AHM=45°=∠BAD,
∴HM=AM,
∵∠1=∠3=22.5°,HD⊥BC,HM⊥AB,
∴DH=HM=AM,
在△BMH和△BHD中
|
∴△BMH≌△BHD,
∴BM=BD,
∴AB=BM+AM=BD+DH,∴①②③正确;
故选D.
点评:本题考查了全等三角形的性质和判定,角平分线性质,三角形内角和定理的应用,主要考查学生综合运用定理进行推理的能力,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
用科学记数法表示为1.999×103的数是( )
| A、1999 |
| B、199.9 |
| C、0.001999 |
| D、19990 |
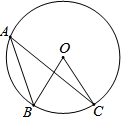 如图,点A、B、C在⊙O上,∠B=52°,∠C=18°,则∠A的度数为( )
如图,点A、B、C在⊙O上,∠B=52°,∠C=18°,则∠A的度数为( )| A、30° | B、20° |
| C、34° | D、28° |
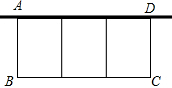 如图,某农场要利用一面墙(墙长为50米)建蔬菜实验田,用120米的围栏围成总面积为800平方米的三个大小、形状完全相同的矩形实验田,种植三种不同的蔬菜,求实验田的边长AB、BC各为多少米?
如图,某农场要利用一面墙(墙长为50米)建蔬菜实验田,用120米的围栏围成总面积为800平方米的三个大小、形状完全相同的矩形实验田,种植三种不同的蔬菜,求实验田的边长AB、BC各为多少米?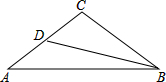 如图,△ABC中,CA=CB,∠ACB=108°,BD平分∠ABC交AC于D,求证:AB=AD+BC.
如图,△ABC中,CA=CB,∠ACB=108°,BD平分∠ABC交AC于D,求证:AB=AD+BC. 已知:DA⊥AB,CA⊥AE,AB=AE,AC=AD,求证:DE=BC.
已知:DA⊥AB,CA⊥AE,AB=AE,AC=AD,求证:DE=BC.