题目内容
9.如果f(x)=$\frac{1}{{\sqrt{3}-\sqrt{x}}}$,那么f(2)=$\sqrt{3}+\sqrt{2}$.分析 将x=2代入公式,再分母有理化可得.
解答 解:当x=2时,f(2)=$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\frac{\sqrt{3}+\sqrt{2}}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}$=$\sqrt{3}+\sqrt{2}$,
故答案为:$\sqrt{3}+\sqrt{2}$.
点评 本题主要考查函数的求值,(1)当已知函数解析式时,求函数值就是求代数式的值;(2)函数值是唯一的,而对应的自变量可以是多个.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
20.在反比例函数y=$\frac{1-3k}{x}$的图象上有两点A(x1,y1),B(x2,y2),当0<x1<x2时,有y1>y2,则k的取值范围是( )
| A. | k$>\frac{1}{3}$ | B. | k$<\frac{1}{3}$ | C. | k$≥\frac{1}{3}$ | D. | k$≤\frac{1}{3}$ |
17.“一方有难,八方支援”,雅安芦山4•20地震后,某单位为一中学捐赠了一批新桌椅,学校组织初一年级200名学生搬桌椅.规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)的套数为( )
| A. | 60 | B. | 70 | C. | 80 | D. | 90 |
4.在公园的O处附近有E、F、G、H四棵树,位置如图所示(图中小正方形的边长均相等)现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E、F、G、H四棵树中需要被移除的为( )
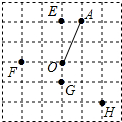

| A. | E、F、G | B. | F、G、H | C. | G、H、E | D. | H、E、F |
14. 在1-7月份,某种水果的每斤进价与售价的信息如图所示,则出售该种水果每斤利润最大的月份是( )
在1-7月份,某种水果的每斤进价与售价的信息如图所示,则出售该种水果每斤利润最大的月份是( )
 在1-7月份,某种水果的每斤进价与售价的信息如图所示,则出售该种水果每斤利润最大的月份是( )
在1-7月份,某种水果的每斤进价与售价的信息如图所示,则出售该种水果每斤利润最大的月份是( )| A. | 3月份 | B. | 4月份 | C. | 5月份 | D. | 6月份 |
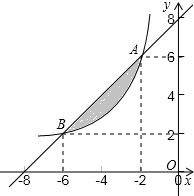 如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上.
如图A、B两点在函数y=$\frac{k}{x}$(x<0)的图象上. 一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为$\frac{40+40\sqrt{3}}{3}$海里/小时.
一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为$\frac{40+40\sqrt{3}}{3}$海里/小时.