题目内容
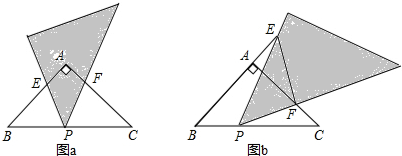
 如图,在△ABC中,E是AB边上的点,DE⊥BC于D,连接AD,EC相交于点F,且AD=AC,∠B=∠ECB.
如图,在△ABC中,E是AB边上的点,DE⊥BC于D,连接AD,EC相交于点F,且AD=AC,∠B=∠ECB.(1)求证:△ABC∽△FCD;
(2)若AC=2,求FD的长.
考点:相似三角形的判定与性质
专题:计算题
分析:(1)由AD=AC,利用等边对等角得到一对角相等,再由已知角相等,利用两对对应角相等的三角形相似即可得证;
(2)由(1)结论,利用相似三角形对应边成比例列出关系式,根据D为BC的中点,由AC的长求出FD的长即可.
(2)由(1)结论,利用相似三角形对应边成比例列出关系式,根据D为BC的中点,由AC的长求出FD的长即可.
解答: (1)证明:∵AD=AC,
(1)证明:∵AD=AC,
∴∠ADC=∠ACB,
∵∠B=∠ECB,
∴△ABC∽△FCD;
(2)解:∵△ABC∽△FCD,且D为BC中点,即BC=2CD,
∴
=
,即
=
,
则FD=1.
 (1)证明:∵AD=AC,
(1)证明:∵AD=AC,∴∠ADC=∠ACB,
∵∠B=∠ECB,
∴△ABC∽△FCD;
(2)解:∵△ABC∽△FCD,且D为BC中点,即BC=2CD,
∴
| CD |
| BC |
| FD |
| AC |
| 1 |
| 2 |
| FD |
| 2 |
则FD=1.
点评:此题考查了相似三角形的判定与性质,等腰三角形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )
如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )| A、4 | ||
B、
| ||
C、
| ||
D、
|
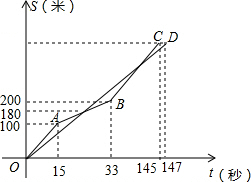 如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )| A、乙比甲先到终点 |
| B、比赛进行到29.4秒时,两人出发后第一次相遇 |
| C、乙测试的速度随时间增加而增大 |
| D、比赛全程甲的测试速度始终比乙的测试速度快 |
在平面直角坐标系中,点O是坐标原点,过点A(1,2)的直线y=kx+b与x轴交于点B,且S△AOB=4,则k的值是( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
 如图,量角器外缘边上A、P、Q三点,它们所表示的读数分别是180°,76°,26°,则∠PAQ的大小为
如图,量角器外缘边上A、P、Q三点,它们所表示的读数分别是180°,76°,26°,则∠PAQ的大小为
 己知:如图,AD⊥BC,垂足为D,矩形EFGH的顶点都在△ABC的边上,且BC=36cm,AD=12cm,
己知:如图,AD⊥BC,垂足为D,矩形EFGH的顶点都在△ABC的边上,且BC=36cm,AD=12cm,