题目内容
2. 如图,在△ABC中,AD、BD、BE、EC的长度分别为1、4、2、5,AF的长度是FC的2倍.如果△ABC的面积是210平方厘米,求△DEF的面积.
如图,在△ABC中,AD、BD、BE、EC的长度分别为1、4、2、5,AF的长度是FC的2倍.如果△ABC的面积是210平方厘米,求△DEF的面积.
分析 根据题意,连接AE,BF,CD,根据等高的三角形面积与底的正比关系,即可知道△ADF,△BDE,△EFC与△ABC的关系,进一步得到△DEF与△ABC的关系,即可求得△DEF的面积.
解答 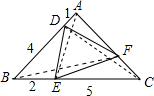 解:连接AE、BF、CD,
解:连接AE、BF、CD,
∵AD、BD、BE、EC的长度分别为1、4、2、5,AF=2CF,△ABC的面积是210平方厘米,
∴S△BDE=$\frac{4}{5}$S△ABE=$\frac{4}{5}$×$\frac{2}{7}$S△ABC=$\frac{8}{35}$S△ABC=48,
S△EFC=$\frac{5}{7}$S△BCF=$\frac{5}{7}$×$\frac{1}{3}$S△ABC=$\frac{5}{21}$S△ABC=50,
S△ADF=$\frac{2}{3}$S△ADC=$\frac{2}{3}$×$\frac{1}{5}$S△ABC=$\frac{2}{15}$S△ABC=28,
∴S△DEF=S△ABC-(S△BDE+S△EFC+S△ADF)
=210-(48+50+28)
=84(平方厘米).
点评 本题考查了三角形面积与底的正比关系,关键是熟练高一定时,三角形的面积与底成正比关系的灵活运用.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图所示,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为45°.
如图所示,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为45°.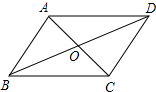 如图,在四边形ABCD中,AB=CD,AD=BC,AC与BD相交于O点,则由“SSS”可判定( )对三角形全等.
如图,在四边形ABCD中,AB=CD,AD=BC,AC与BD相交于O点,则由“SSS”可判定( )对三角形全等.