题目内容
14．计算：$\frac{1}{a（a+1）}$+$\frac{1}{（a+1）（a+2）}$+…+$\frac{1}{（a+2013）（a+2014）}$．分析 根据拆项法，可得互为相反数的项，根据分式的加减，可得答案．
解答 解：原式=$\frac{1}{a}$-$\frac{1}{a+1}$+$\frac{1}{a+1}$-$\frac{1}{a+2}$+…+$\frac{1}{a+2013}$-$\frac{1}{a+2014}$
=$\frac{1}{a}$-$\frac{1}{a+2014}$
=$\frac{2014}{a（a+2014）}$．
点评 本题考查了分式的加减，利用$\frac{1}{a（a+1）}$=$\frac{1}{a}$-$\frac{1}{a+1}$是解题关键．
练习册系列答案
相关题目
4．函数y=$\frac{2}{x}$的图象过点（x1，y1），（x2，y2）且x2＞x1＞0，则有（ ）
| A． | y1＞y2＞0 | B． | y2＞y1＞0 | C． | y1＜y2＜0 | D． | y2＜y1＜0 |
如图，在△ABC中，AD、BD、BE、EC的长度分别为1、4、2、5，AF的长度是FC的2倍．如果△ABC的面积是210平方厘米，求△DEF的面积．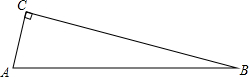
在Rt△ABC中，∠C=90°，∠B=15°，若AC=1，求AB的长．