题目内容
12. 如图所示,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为45°.
如图所示,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为45°.
分析 分别在格点三角形中,根据勾股定理即可得到AB,BC,AC的长度,继而可得出∠ABC的度数.
解答 解:如图,连接AC.
根据勾股定理可以得到:AC=BC=$\sqrt{5}$,AB=$\sqrt{10}$,
∵($\sqrt{5}$)2+($\sqrt{5}$)2=($\sqrt{10}$)2,即AC2+BC2=AB2,
∴△ABC是等腰直角三角形.
∴∠ABC=45°.
故答案为:45°.
点评 本题考查了勾股定理,判断△ABC是等腰直角三角形是解决本题的关键,注意在格点三角形中利用勾股定理.

练习册系列答案
相关题目
2.下列结论不正确的是( )
| A. | 等腰三角形底边上的高、中线、角平分线互相重合 | |
| B. | 等腰三角形内角可以是钝角 | |
| C. | 等腰三角形的底角只能是锐角 | |
| D. | 等边三角形是特殊的等腰三角形 |
3.下列变形属于分解因式的是( )
| A. | 2x2-4x+1=2x(x-2)+1 | B. | m(a+b+c)=ma+mb+mc | ||
| C. | x2-y2=(x+y)(x-y) | D. | (m-n)(b+a)=(b+a)(m-n) |
7.已知a<b,则下列式子正确的是( )
| A. | a-1>b-1 | B. | -3a<-3b | C. | -2a>-2b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
4.函数y=$\frac{2}{x}$的图象过点(x1,y1),(x2,y2)且x2>x1>0,则有( )
| A. | y1>y2>0 | B. | y2>y1>0 | C. | y1<y2<0 | D. | y2<y1<0 |
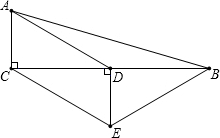 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.求证:AD=BE.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.求证:AD=BE. 已知:如图,CD=AB且CD∥AB,E、F是直线AC上两点,且AE=CF.求证:
已知:如图,CD=AB且CD∥AB,E、F是直线AC上两点,且AE=CF.求证: 如图,在△ABC中,AD、BD、BE、EC的长度分别为1、4、2、5,AF的长度是FC的2倍.如果△ABC的面积是210平方厘米,求△DEF的面积.
如图,在△ABC中,AD、BD、BE、EC的长度分别为1、4、2、5,AF的长度是FC的2倍.如果△ABC的面积是210平方厘米,求△DEF的面积.