题目内容
13.计算(1)${({\frac{{{a^2}b}}{-c}})^2}•{({-\frac{c^2}{ab}})^2}÷{({\frac{bc}{a}})^4}$;
(2)先化简,再选择使原式有意义而你喜欢的数代入求值:$\frac{1}{x+1}-\frac{x+2}{{{x^2}-1}}•\frac{{{x^2}-2x+1}}{{x{\;}^2+4x+4}}$.
分析 (1)直接根据分式的乘除法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.
解答 解:(1)原式=$\frac{{a}^{4}{b}^{2}}{{c}^{2}}$•$\frac{{c}^{4}}{{a}^{2}{b}^{2}}$•$\frac{{a}^{4}}{{b}^{4}{c}^{4}}$
=a2c2•$\frac{{a}^{4}}{{b}^{4}{c}^{4}}$
=$\frac{a^6}{{{b^4}{c^2}}}$;
(2)原式=$\frac{1}{x+1}$-$\frac{x+2}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{(x+2)^{2}}$
=$\frac{1}{x+1}$-$\frac{x-1}{(x+1)(x+2)}$
=$\frac{x+2-x+1}{(x+1)(x+2)}$
=$\frac{3}{(x+1)(x+2)}$,
当x=0时,原式=$\frac{3}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
3.下列变形属于分解因式的是( )
| A. | 2x2-4x+1=2x(x-2)+1 | B. | m(a+b+c)=ma+mb+mc | ||
| C. | x2-y2=(x+y)(x-y) | D. | (m-n)(b+a)=(b+a)(m-n) |
4.函数y=$\frac{2}{x}$的图象过点(x1,y1),(x2,y2)且x2>x1>0,则有( )
| A. | y1>y2>0 | B. | y2>y1>0 | C. | y1<y2<0 | D. | y2<y1<0 |
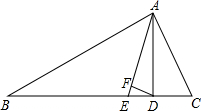 如图,在△ABC中,∠B=25°,∠C=65°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE.
如图,在△ABC中,∠B=25°,∠C=65°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE. 如图,在△ABC中,AD、BD、BE、EC的长度分别为1、4、2、5,AF的长度是FC的2倍.如果△ABC的面积是210平方厘米,求△DEF的面积.
如图,在△ABC中,AD、BD、BE、EC的长度分别为1、4、2、5,AF的长度是FC的2倍.如果△ABC的面积是210平方厘米,求△DEF的面积.