题目内容
15.已知a+$\frac{1}{a}=3$,求代数式$\frac{{a}^{4}-3{a}^{2}+1}{{a}^{2}}$的值.分析 先把原式变形为a2-3+$\frac{1}{{a}^{2}}$,再根据完全平方公式得到原式=(a+$\frac{1}{a}$)2-5,然后利用整体代入的方法计算.
解答 解:原式=a2-3+$\frac{1}{{a}^{2}}$
=(a+$\frac{1}{a}$)2-5,
当a+$\frac{1}{a}=3$时,原式=32-5=4.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.下列计算正确的是( )
| A. | a3+a4=a7 | B. | (a3)4=a7 | C. | (-a2b3)3=a6b9 | D. | 2a4•3a5=6a9 |
5.下列图形中,是中心对称图形,但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
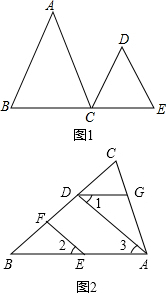 (1)已知:如图,AB∥CD,∠A=∠D.试说明AC∥DE成立的理由.下面是某同学进行的推理.请你将他的推理过程补充完整.
(1)已知:如图,AB∥CD,∠A=∠D.试说明AC∥DE成立的理由.下面是某同学进行的推理.请你将他的推理过程补充完整.