题目内容
3.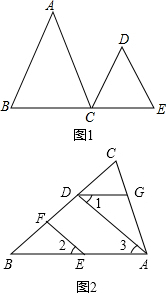 (1)已知:如图,AB∥CD,∠A=∠D.试说明AC∥DE成立的理由.下面是某同学进行的推理.请你将他的推理过程补充完整.
(1)已知:如图,AB∥CD,∠A=∠D.试说明AC∥DE成立的理由.下面是某同学进行的推理.请你将他的推理过程补充完整.解:∵AB∥CD (已知)
∴∠A=∠ACD(两直线平行,内错角相等)
又∵∠A=∠D (已知)
∴∠ACD=∠D (等量代换)
∴AC∥DE (内错角相等,两直线平行)(已知)
(2)如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整
解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2 (已知)
∴∠l=∠3
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
又∵∠BAC=70°(已知)
∴∠AGD=110°.
分析 (1)由平行线的性质和已知条件得出∠ACD=∠D,即可得出结论;
(2)由平行线的性质和已知条件得出∠1=∠3,证出AB∥DG,再由平行线的性质即可得出结果.
解答 (1)解:∵AB∥CD (已知)
∴∠A=∠ACD (两直线平行,内错角相等)
又∵∠A=∠D (已知)
∴∠ACD=∠D (等量代换)
∴AC∥DE (内错角相等,两直线平行)
故答案为:ACD,两直线平行,内错角相等;ACD,D,内错角相等,两直线平行;
(2)解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2 (已知)
∴∠l=∠3
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
又∵∠BAC=70°(已知)
∴∠AGD=110°.
故答案为:∠3,两直线平行,同位角相等;DG,内错角相等,两直线平行;∠AGD,两直线平行,同旁内角互补;110°
点评 本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质,注意它们之间的区别.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
14.化简$\sqrt{27}$的结果是( )
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 9 |
18.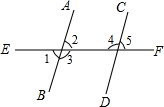 如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
 如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8. 如图,直线b、c被直线a所截,则∠1与∠2是( )
如图,直线b、c被直线a所截,则∠1与∠2是( )
 如图,直线b、c被直线a所截,则∠1与∠2是( )
如图,直线b、c被直线a所截,则∠1与∠2是( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 对顶角 |
12.若x,y都是实数,且$\sqrt{2x-1}$+$\sqrt{2-4x}$+y=4,则xy的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 2 | D. | 不能确定 |
13.计算-5+2的结果是( )
| A. | -7 | B. | -3 | C. | 3 | D. | 7 |
 6,0),O(0,0),则cos∠OBC的值为( )
6,0),O(0,0),则cos∠OBC的值为( )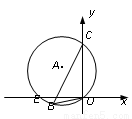
 B.
B.  C.
C.  D.
D.