题目内容
5．直角三角形的两直角边均扩大到原来的两倍，则斜边扩大到原来的（ ）| A． | 8倍 | B． | 4倍 | C． | 2倍 | D． | 6倍 |
分析 设直角三角形两直角边分别为a，b，斜边为c，根据勾股定理列出关系式，将两直角边变形为2a与2b，利用勾股定理求出变化后的斜边，即可做出判断．
解答 解：设直角三角形两直角边分别为a，b，斜边为c，
根据勾股定理得：a2+b2=c2，
若两直角边扩大2倍，变为2a与2b，
根据勾股定理得：斜边为$\sqrt{（2a）^{2}+（2b）^{2}}$=2$\sqrt{{a}^{2}+{b}^{2}}$=2c，
则斜边扩大到原来的2倍．
故选C．
点评 此题考查了勾股定理，勾股定理很好的建立了直角三角形三边的关系，熟练掌握勾股定理是解本题的关键．
练习册系列答案
相关题目
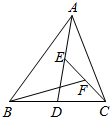如图，在△ABC中，点D、E、F分别为BC、AD、CE的中点．若S△BFC=1，则S△ABC=4．
如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象经过A（0，-2），B（1，0）两点，与反比例函数$y=\frac{m}{x}$（m≠0）的图象在第一象限内交于点M，若△OBM的面积是2．
如图，△ABC中，∠ACB=90°，延长AC到D，使得CD=CB，过点D作DE⊥AB于点E，交BC于F．求证：AB=DF．