题目内容
13. 如图,△ABC中,∠ACB=90°,延长AC到D,使得CD=CB,过点D作DE⊥AB于点E,交BC于F.求证:AB=DF.
如图,△ABC中,∠ACB=90°,延长AC到D,使得CD=CB,过点D作DE⊥AB于点E,交BC于F.求证:AB=DF.
分析 根据余角的定义得出∠D=∠B,再根据ASA证明△DFC和△BAC全等,最后根据全等三角形的性质证明即可.
解答 证明:∵DE⊥AB,
∴∠DEA=90°,
∵∠ACB=90°,
∴∠DEA=∠ACB,
∴∠D=∠B,
在△DCF和△ACB中,
$\left\{\begin{array}{l}{∠DCB=∠ACB}\\{DC=BC}\\{∠B=∠D}\end{array}\right.$,
∴△DCF≌△ACB(ASA),
∴AB=DF.
点评 此题考查全等三角形的判定和性质,关键是利用互余得出∠D=∠B,再根据ASA证明三角形全等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.据海关统计,2015年前两个月,我国进出口总值为37900亿元人民币,将37900用科学记数法表示为( )
| A. | 3.79×102 | B. | 0.379×105 | C. | 3.79×104 | D. | 379×102 |
1.2015年清明小长假延庆县的旅游收入约为1900万,将1900用科学记数法表示应为( )
| A. | 19×102 | B. | 1.9×103 | C. | 1.9×104 | D. | 0.19×104 |
8.某校学生参加体育测试,某小组10名同学的完成引体向上的个数如下表,
这10名同学引体向上个数的众数与中位数依次是( )
| 完成引体向上的个数 | 10 | 9 | 8 | 7 |
| 人 数 | 1 | 1 | 3 | 5 |
| A. | 7和7.5 | B. | 7和8 | C. | 7.5和9 | D. | 8和9 |
5.直角三角形的两直角边均扩大到原来的两倍,则斜边扩大到原来的( )
| A. | 8倍 | B. | 4倍 | C. | 2倍 | D. | 6倍 |
3.在六张卡片上分别写有π,$\frac{1}{3}$,1.5,-3,0,$\sqrt{2}$六个数,从中任意抽取一张,卡片上的数为无理数的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
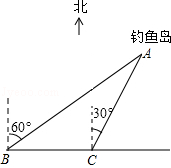 如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近?
如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行50海里与钓鱼岛A的距离最近?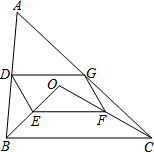 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.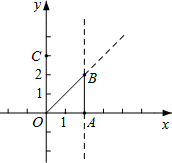 抛物线C1:y=$\frac{1}{2}{x^2}$+bx+c与y轴交于点C(0,3),其对称轴与x轴交于点A(2,0).
抛物线C1:y=$\frac{1}{2}{x^2}$+bx+c与y轴交于点C(0,3),其对称轴与x轴交于点A(2,0).