题目内容
16. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数$y=\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象经过A(0,-2),B(1,0)两点,与反比例函数$y=\frac{m}{x}$(m≠0)的图象在第一象限内交于点M,若△OBM的面积是2.(1)求一次函数和反比例函数的表达式;
(2)若点P是x轴上一点,且满足△AMP是以AM为直角边的直角三角形,请直接写出点P的坐标.
分析 (1)根据一次函数y=k1x+b的图象经过A(0,-2),B(1,0)可得到关于b、k的方程组,进而可得到一次函数的解析式,设M(p,q)作MD⊥x轴于点D,由△OBM的面积为2可求出q的值,将M(p,4)代入y=2x-2求出p的值,由M(3,4)在双曲线$y=\frac{m}{x}$(m≠0)上即可求出m的值,进而求出其反比例函数的解析式;
(2)作MD⊥x轴于D,分两种情况:①过点M(3,4)作MP⊥AM交x轴于点P,由MD⊥BP可求出∠PMD=∠MBD=∠ABO,再由锐角三角函数的定义可得出OP的值,进而可得出结论;②过点A(0,-2)作AP⊥AM交x轴于点P,由MD⊥BP可求出∠MBD=∠ABO=∠PAO,再由锐角三角函数的定义可得出OP的值,进而可得出结论.
解答 解:(1)∵直线y=kx+b过A(0,-2),B(1,0)两点
∴$\left\{\begin{array}{l}{b=-2}\\{k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-2}\end{array}\right.$
∴一次函数的表达式为y=2x-2,
∴设M(p,q),作MD⊥x轴于点D
∵S△OBM=2,
∴$\frac{1}{2}$OB•MD=2,
∴$\frac{1}{2}$q=2,
∴q=4,
∴将M(p,4)代入y=2x-2得4=2p-2,
∴p=3
∵M(3,4)在双曲线$y=\frac{m}{x}$(m≠0)上,
∴4=$\frac{m}{3}$,
∴m=12,
∴反比例函数的表达式为:y=$\frac{12}{x}$;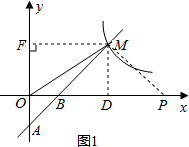
(2)作MD⊥x轴于D,
①如图1,过点M(3,4)作MP⊥AM交x轴于点P,
∵MD⊥BP,
∴∠PMD=∠MBD=∠ABO
∴tan∠PMD=tan∠MBD=tan∠ABO=$\frac{OA}{OB}$=2,
∴在Rt△PDM中,$\frac{PD}{MD}$=2,
∴PD=2MD=8,
∴OP=OD+PD=11或OP=PD-OD=8-3=5
∴当PM⊥AM,此时点P的坐标为(11,0).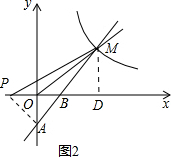
②如图2,过点A(0,-2)作AP⊥AM交x轴于点P,
∵MD⊥BP,
∴∠MBD=∠ABO=∠PAO,
∴tan∠PAO=tan∠MBD=tan∠ABO=$\frac{OA}{OB}$=2,
∴在Rt△POA中,$\frac{OP}{OA}$=2,
∴OP=4,
∴当PA⊥AM,此时点P的坐标为(-4,0).
点评 本题考查的是反比例函数与一次函数的交点问题,涉及到的知识点为用待定系数法求一次函数与反比例函数的解析式、锐角三角函数的定义,熟知以上知识是解答此题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 3.79×102 | B. | 0.379×105 | C. | 3.79×104 | D. | 379×102 |
| A. | 19×102 | B. | 1.9×103 | C. | 1.9×104 | D. | 0.19×104 |
| 完成引体向上的个数 | 10 | 9 | 8 | 7 |
| 人 数 | 1 | 1 | 3 | 5 |
| A. | 7和7.5 | B. | 7和8 | C. | 7.5和9 | D. | 8和9 |
| A. | 8倍 | B. | 4倍 | C. | 2倍 | D. | 6倍 |
 如图,某小区规划在一个长80m、宽50m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,使花草的种植面积共为3800m2.设通道的宽为xm,可依题意列得方程:(80-2x)(50-x)=3800.
如图,某小区规划在一个长80m、宽50m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,使花草的种植面积共为3800m2.设通道的宽为xm,可依题意列得方程:(80-2x)(50-x)=3800.