题目内容
某市天然气公司在一些居民小区安装天然气管道时,采用一种鼓励居民使用天然气的收费办法,若整个小区每户都安装,收整体初装费10 000元,再对每户收费500元.某小区住户按这种收费方法全部安装天然气后,每户平均支付不足1 000元,则这个小区的住户数( )
A. 至少20户 B. 至多20户 C. 至少21户 D. 至多21户
C
【解析】试题分析：设这个小区的住户数为x户，得共需安装费10000+500x，由每户平均支付不足1000元，则总体安装费不足1000x，列不等式求解即可．
【解析】
设这个小区的住户数为x户，
则10000+500x<1000x，解得x>20．
∵x是整数，∴这个小区的住户数至少21户．
故选C．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
相关题目
计算
【解析】试题分析：分母相同，按照同分母分式加减的法则进行计算，分子合并同类项后再进行约分化简．
试题解析：
【解析】
原式＝
＝
＝． 求出不等式3x－2≥4(x－1)的所有非负整数解．
不等式的解集是x≤2，故不等式3x－2≥4(x－1)的非负整数解为0,1,2.
【解析】【试题分析】去括号得： 移项得： 合并得： ，系数化为1得：x≤2，所以不等式的非负整数解为0,1,2.
【试题解析】
去括号得：
移项得：
合并得： ，
系数化为1得：x≤2，
所以不等式的非负整数解为0,1,2. 如图，已知AB=AD给出下列条件：
（1）CB=CD （2）∠BAC=∠DAC （3）∠BCA=∠DCA （4）∠B=∠D，
若再添一个条件后，能使△ABC≌△ADC的共有（ ）
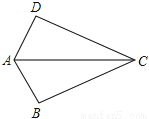
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】∵在△ABC和△ADC中，AB=AD，AC=AC，
∴（1）添加“CB=CD”可由“SSS”判定△ABC≌△ADC；
（2）添加“∠BAC=∠DAC”可由“SAS”判定△ABC≌△ADC；
（3）添加“∠BCA=∠DCA”不能判定△ABC≌△ADC；
（4）添加“∠B=∠D”不能判定△ABC≌△ADC；
即4个条件中，添加（1）和（2）能使△ABC≌... 某商场推出一种购物“金卡”，凭卡在该商场购物可按商品价格的八折优惠，但办理金卡时每张要收100元购卡费，设按标价累计购物金额为x（元），当x＞__时，办理金卡购物省钱．
500
【解析】【解析】
依题意得：x﹣0.8x＞100，解得：x＞500．
即当购物金额大于500元时，办理金卡购物省钱．
故答案为：500． 每年3月12日是植树节，某学校植树小组若干人植树，植树若干棵．若每人植4棵，则余20棵没人植，若每人植8棵，则有一人比其他人植的少（但有树植），问这个植树小组有多少人？共有多少棵树？
这个植树小组有6人去植树，共有4×6+20=44棵树．
【解析】【试题分析】设该校一共有x人去植树，共有y棵树．则根据题意可得：，求解即得
【试题解析】设个植树小组有x人去植树，共有y棵树．
由“每人植4棵，则余20棵没人植”和“若每人植8棵，则有一人比其他人植的少（但有树植）”得：
，将y=4x+20代入第二个式子得：
0＜4x+20﹣8（x﹣1）＜8，
5＜... 不等式x﹣8＞3x﹣5的最大整数解是_________．
﹣2
【解析】不等式x﹣8＞3x﹣5的解集为x＜﹣；
所以其最大整数解是﹣2． 不等式－3x+6＞0的正整数解有（ ）．
A．1个 B．2个 C．3个 D．无数多个
A．
【解析】
试题分析：解不等式得到x＜2，所以x可取的正整数只有1．
故选:A． 如图，在?ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是_______．
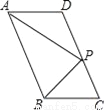
24
【解析】试题分析：∵四边形ABCD是平行四边形，
∴AD∥CB，AB∥CD，
∴∠DAB＋∠CBA＝180°，
又∵AP和BP分别平分∠DAB和∠CBA，
∴∠PAB＋∠PBA＝ (∠DAB＋∠CBA)＝90°，
在△APB中，∠APB＝180°－(∠PAB＋∠PBA)＝90°；
∵AP平分∠DAB，
∴∠DAP＝∠PAB，
∵AB∥CD...