题目内容
某商场推出一种购物“金卡”，凭卡在该商场购物可按商品价格的八折优惠，但办理金卡时每张要收100元购卡费，设按标价累计购物金额为x（元），当x＞__时，办理金卡购物省钱．
500
【解析】【解析】
依题意得：x﹣0.8x＞100，解得：x＞500．
即当购物金额大于500元时，办理金卡购物省钱．
故答案为：500．
活力课时同步练习册系列答案分式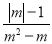
的值为零，则m取值为（ ）
A. m＝±1 B. m＝－1 C. m＝1 D. m的值不存在
B
【解析】试题解析：分式的值为零的条件是分母不为0，分子为0，所以可以得到，可以得到， ，可以得到且，综上所述则m取值为-1
故选B. 甲种蔬菜保鲜适宜的温度是1℃～5℃，乙种蔬菜保鲜适宜的温度是3℃～8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（ ）
A. 1℃～3℃ B. 3℃～5℃ C. 5℃～8℃ D. 1℃～8℃
B
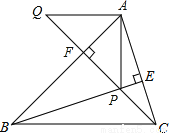
【解析】试题分析：设温度为x℃，由题意得，解得3≤x≤5，故答案选B. 如图，BE、CF是△ABC的高且相交于点P，AQ∥BC交CF延长线于点Q，若有BP=AC，CQ=AB，线段AP与AQ的关系如何？说明理由。
证明见解析
【解析】试题分析：
由BE、CF是△ABC的高，易得∠ABP+∠BPF=90°，∠ACP+∠CPE=90°，结合∠BPF=∠CPE，易得∠ABP=∠ACP，这样结合BP=AC，CQ=AB，即可由“SAS”证得△ACQ≌△PBA，从而可得AP=AQ，∠Q=∠PAF，结合∠PAF+∠APF=90°，可得：∠APF+∠Q=90°，即可得到∠QAP=90°，从而可得AQ⊥AP，由此... 某镇水库的可用水量为12000万m3，假设年降水量不变，能维持该镇16万人20年的用水量．为实施城镇化建设，新迁入了4万人后，水库只能够维持居民15年的用水量．
（1）问：年降水量为多少万m3？每人年平均用水量多少m3？
（2）政府号召节约用水，希望将水库的使用年限提高到25年．则该镇居民人均每年需节约多少m3水才能实现目标？
（3）某企业投入1000万元设备，每天能淡化5000m3海水，淡化率为70%．每淡化1m3海水所需的费用为1.5元，政府补贴0.3元．企业将淡化水以3.2元/m3的价格出售，每年还需各项支出40万元．按每年实际生产300天计算，该企业至少几年后能收回成本（结果精确到个位）？
【解析】
（1）设年降水量为x万m3，每人年平均用水量为ym3，
由题意得，，解得：。
答：年降水量为200万m3，每人年平均用水量为50m3．
（2）设该镇居民人均每年需节约z m3水才能实现目标，
由题意得，12000+25×200=20×25z，解得：z=34。
50﹣34=16m3．
答：设该镇居民人均每年需节约16 m3水才能实现目标。
（3）... 某市天然气公司在一些居民小区安装天然气管道时,采用一种鼓励居民使用天然气的收费办法,若整个小区每户都安装,收整体初装费10 000元,再对每户收费500元.某小区住户按这种收费方法全部安装天然气后,每户平均支付不足1 000元,则这个小区的住户数( )
A. 至少20户 B. 至多20户 C. 至少21户 D. 至多21户
C
【解析】试题分析：设这个小区的住户数为x户，得共需安装费10000+500x，由每户平均支付不足1000元，则总体安装费不足1000x，列不等式求解即可．
【解析】
设这个小区的住户数为x户，
则10000+500x<1000x，解得x>20．
∵x是整数，∴这个小区的住户数至少21户．
故选C． 是否存在整数k，使方程组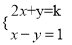
的解中，x大于1，y不大于1，若存在，求出k的值，若不存在，说明理由．
k只能取3，4，5
【解析】【试题分析】解此题时可以解出二元一次方程组中x，y关于k的式子，然后解出k的范围，即可知道k的取值．
【试题解析】解方程组得
∵x大于1，y不大于1从而得不等式组
解之得2＜k≤5
又∵k为整数
∴k只能取3，4，5
答：当k为3，4，5时，方程组的解中，x大于1，y不大于1． 若a＞b＞0，则下列结论正确的是（ ）
A. ﹣a＞﹣b B.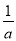 
＞
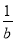C. a3＜0 D. a2＞b2
D
【解析】A、不等式两边都乘﹣1，不等号的方向改变，错误；
B、3＞2＞0，但＜，错误；
C、正数的奇次幂是正数，a3＞0，错误；
D、两个正数，较大的数的平方也大，正确；
故选D. 如图，E是?ABCD的边CD的中点，延长AE交BC的延长线于点F．
（1）求证：△ADE≌△FCE．
（2）若∠BAF=90°，BC=5，EF=3，求CD的长．
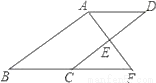
（1）证明过程见解析；（2）8.
【解析】试题分析：（1）由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE=∠F，∠D=∠ECF，由AAS证明△ADE≌△FCE即可；（2）由全等三角形的性质得出AE=EF=3，由平行线的性质证出∠AED=∠BAF=90°，由勾股定理求出DE，即可得出CD的长．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AD∥BC，AB∥CD，
...