��Ŀ����
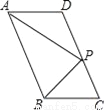
��ͼ����?ABCD�У�P��CD����һ�㣬��AP��BP�ֱ�ƽ�֡�DAB�͡�CBA����AD=5��AP=8�����APB���ܳ���_______��
 24
��������������������ı���ABCD��ƽ���ı��Σ�
��AD��CB��AB��CD��
���DAB����CBA��180�㣬
�֡�AP��BP�ֱ�ƽ�֡�DAB�͡�CBA��
���PAB����PBA�� (��DAB����CBA)��90�㣬
�ڡ�APB�У���APB��180�㣭(��PAB����PBA)��90�㣻
��APƽ�֡�DAB��
���DAP����PAB��
��AB��CD...
24
��������������������ı���ABCD��ƽ���ı��Σ�
��AD��CB��AB��CD��
���DAB����CBA��180�㣬
�֡�AP��BP�ֱ�ƽ�֡�DAB�͡�CBA��
���PAB����PBA�� (��DAB����CBA)��90�㣬
�ڡ�APB�У���APB��180�㣭(��PAB����PBA)��90�㣻
��APƽ�֡�DAB��
���DAP����PAB��
��AB��CD...
 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�ij����Ȼ����˾��һЩ����С����װ��Ȼ���ܵ�ʱ,����һ�ֹ�������ʹ����Ȼ�����շѰ취,������С��ÿ������װ,�������װ��10 000Ԫ,�ٶ�ÿ���շ�500Ԫ.ijС��ס���������շѷ���ȫ����װ��Ȼ����,ÿ��ƽ��֧������1 000Ԫ,�����С����ס����( ��)
A. ����20�� B. ����20�� C. ����21�� D. ����21��
 C
����������������������С����ס����Ϊx�����ù��谲װ��10000+500x����ÿ��ƽ��֧������1000Ԫ�������尲װ�Ѳ���1000x���в���ʽ��⼴�ɣ�
��������
�����С����ס����Ϊx����
��10000+500x<1000x�����x>20��
��x�������������С����ס��������21����
��ѡC��
C
����������������������С����ס����Ϊx�����ù��谲װ��10000+500x����ÿ��ƽ��֧������1000Ԫ�������尲װ�Ѳ���1000x���в���ʽ��⼴�ɣ�
��������
�����С����ס����Ϊx����
��10000+500x<1000x�����x>20��
��x�������������С����ס��������21����
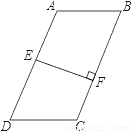
��ѡC�� ��ͼ�����ı���ABCD�У�AB��DC��E��AD�е㣬EF��BC�ڵ�F��BC=5��EF=3��
��1����AB=DC�����ı���ABCD�����S=__��
��2����AB��DC�����ʱ�ı���ABCD�����S��__S���á�������=��������գ���
 (1)15����2��=��
�������������������1����AB=DC��AB��DC��
���ı���ABCD��ƽ���ı��Σ�
���ı���ABCD�����S=5��3=15��
��2����ͼ������EC���ӳ�CD��BE���ڵ�P��
��E��AD�е㣬
��AE=DE��
�֡�AB��CD��
���ABE=��P����A=��PDE��
�ڡ�ABE�͡�DPE�У�
�ߣ�
���ABE�ա�D...
(1)15����2��=��
�������������������1����AB=DC��AB��DC��
���ı���ABCD��ƽ���ı��Σ�
���ı���ABCD�����S=5��3=15��
��2����ͼ������EC���ӳ�CD��BE���ڵ�P��
��E��AD�е㣬
��AE=DE��
�֡�AB��CD��
���ABE=��P����A=��PDE��
�ڡ�ABE�͡�DPE�У�
�ߣ�
���ABE�ա�D... ��ͼ���ȱߡ�ABC�ı߳���2��D��E�ֱ�ΪAB��AC���е㣬�ӳ�BC����F��ʹCF=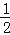 BC������CD��EF��
BC������CD��EF��
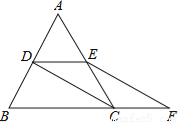
��1����֤��DE=CF��
��2����EF�ij���
 ��������
�������������������1��ֱ��������������λ�߶����ó�DEBC�������ó�DE=FC��
��2������ƽ���ı��ε��ж������ʵó�DC=EF���������õȱ������ε������Լ����ɶ����ó�EF�ij�
�����������1��֤������D��E�ֱ�ΪAB��AC���е㣬 ��DEBC��
���ӳ�BC����F��ʹCF=BC�� ��DEFC�� ��DE=CF��
��2����������
��DEFC�� ���ı���DE...
��������
�������������������1��ֱ��������������λ�߶����ó�DEBC�������ó�DE=FC��
��2������ƽ���ı��ε��ж������ʵó�DC=EF���������õȱ������ε������Լ����ɶ����ó�EF�ij�
�����������1��֤������D��E�ֱ�ΪAB��AC���е㣬 ��DEBC��
���ӳ�BC����F��ʹCF=BC�� ��DEFC�� ��DE=CF��
��2����������
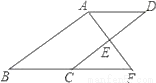
��DEFC�� ���ı���DE... ��ͼ��E��?ABCD�ı�CD���е㣬�ӳ�AE��BC���ӳ����ڵ�F��
��1����֤����ADE�ա�FCE��
��2������BAF=90�㣬BC=5��EF=3����CD�ij���
 ��1��֤�����̼���������2��8.
�������������������1����ƽ���ı��ε����ʵó�AD��BC��AB��CD��֤����DAE=��F����D=��ECF����AAS֤����ADE�ա�FCE���ɣ���2����ȫ�������ε����ʵó�AE=EF=3����ƽ���ߵ�����֤����AED=��BAF=90�㣬�ɹ��ɶ������DE�����ɵó�CD�ij���
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AD��BC��AB��CD��
...
��1��֤�����̼���������2��8.
�������������������1����ƽ���ı��ε����ʵó�AD��BC��AB��CD��֤����DAE=��F����D=��ECF����AAS֤����ADE�ա�FCE���ɣ���2����ȫ�������ε����ʵó�AE=EF=3����ƽ���ߵ�����֤����AED=��BAF=90�㣬�ɹ��ɶ������DE�����ɵó�CD�ij���
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AD��BC��AB��CD��
... ��ͼ����?ABCD�ضԽ���AC�۵���ʹ��B����B�䴦������1=��2=44�㣬���BΪ��������
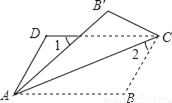
A. 66�� B. 104�� C. 114�� D. 124��
 C
��������������������ı���ABCD��ƽ���ı��Σ�
��AB��CD��
���ACD=��BAC��
���۵������ʵã���BAC=��B��AC��
���BAC=��ACD=��B��AC=
���B=180��-��2-��BAC=180��-44��-22��=114�㣻
��ѡC��
C
��������������������ı���ABCD��ƽ���ı��Σ�
��AB��CD��
���ACD=��BAC��
���۵������ʵã���BAC=��B��AC��
���BAC=��ACD=��B��AC=
���B=180��-��2-��BAC=180��-44��-22��=114�㣻
��ѡC�� ���ı��ε��ڽǺ͵���a������ε���Ǻ͵���b����a��b�Ĺ�ϵ�ǣ�������
A. a��b B. a=b C. a��b D. b=a+180��
 B
�����������ı��ε��ڽǺ͵���a��
��a=��4��2��•180��=360�㣮
������ε���Ǻ͵���b��
��b=360�㣬
��a=b��
��ѡB��
B
�����������ı��ε��ڽǺ͵���a��
��a=��4��2��•180��=360�㣮
������ε���Ǻ͵���b��
��b=360�㣬
��a=b��
��ѡB�� ��ͼ���ڡ�ABC�У���ABC=90�㣬AB=8��BC=6����DE�ǡ�ABC����λ�ߣ��ӳ�DE����ABC����ǡ�ACM��ƽ�����ڵ�F�����߶�DF�ij�Ϊ���� ����
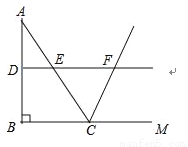
A. 7 B. 8 C. 9 D. 10
 B
�������������������RT��ABC�У��ߡ�ABC=90�㣬AB=8��BC=6����AC===10����DE�ǡ�ABC����λ�ߣ���DF��BM��DE=BC=3�����EFC=��FCM���ߡ�FCE=��FCM�����EFC=��ECF����EC=EF=AC=5����DF=DE+EF=3+5=8����ѡB��
B
�������������������RT��ABC�У��ߡ�ABC=90�㣬AB=8��BC=6����AC===10����DE�ǡ�ABC����λ�ߣ���DF��BM��DE=BC=3�����EFC=��FCM���ߡ�FCE=��FCM�����EFC=��ECF����EC=EF=AC=5����DF=DE+EF=3+5=8����ѡB�� ���κ���y=ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
X | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��ۣ�
��ac��0��
�Ƶ�x��1ʱ��y��ֵ��xֵ���������С��
��3�Ƿ���ax2+��b��1��x+c=0��һ������
�ȵ���1��x��3ʱ��ax2+��b��1��x+c��0��
������ȷ�ĸ���Ϊ�� ��
A. 4�� B. 3�� C. 2�� D. 1��
 B
�����������������-1��-1������0,3������1,5����
��
���,y=-.�Գ���,,
(1)��ȷ����2���������£��Գ��ᣬx��1ʱy�������ټ�С,����3��+2,��ã� .��ȷ����4��+2,�����ɣ�3���õ�������x��Ľ��㣬��ͼ֪����1��x��3ʱ,y>0��ȷ.
���ԣ�1����3����4����ȷ.ѡB.
B
�����������������-1��-1������0,3������1,5����
��
���,y=-.�Գ���,,
(1)��ȷ����2���������£��Գ��ᣬx��1ʱy�������ټ�С,����3��+2,��ã� .��ȷ����4��+2,�����ɣ�3���õ�������x��Ľ��㣬��ͼ֪����1��x��3ʱ,y>0��ȷ.
���ԣ�1����3����4����ȷ.ѡB. 
