题目内容
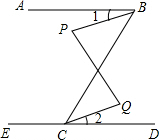 如图,已知∠P=∠Q,∠1=∠2,AB与ED平行吗?为什么?
如图,已知∠P=∠Q,∠1=∠2,AB与ED平行吗?为什么?考点:平行线的判定
专题:常规题型
分析:根据内错角相等,两直线平行由∠P=∠Q得到PB∥CQ,再根据平行线的性质得∠PBC=∠BCQ,由于∠1=∠2,根据等式的性质得∠PBC+∠1=∠BCQ+∠2,即∠ABC=∠DCB,然后根据平行线的判定方法即可得到AB∥ED.
解答:解:AB∥ED.理由如下:
∵∠P=∠Q,
∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠2,
∴∠PBC+∠1=∠BCQ+∠2,
即∠ABC=∠DCB,
∴AB∥ED.
∵∠P=∠Q,
∴PB∥CQ,
∴∠PBC=∠BCQ,
∵∠1=∠2,
∴∠PBC+∠1=∠BCQ+∠2,
即∠ABC=∠DCB,
∴AB∥ED.
点评:本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式组
的解集在数轴上表示为( )
|
A、 |
B、 |
C、 |
D、 |
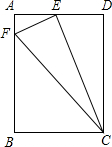 如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE).
如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE).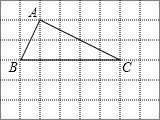 如图,在边长为1个单位长度的小正方形组成的网格中,按要求作图.
如图,在边长为1个单位长度的小正方形组成的网格中,按要求作图.